题目内容
抛物线y=ax2+bx+c的顶点在第一象限与X轴的两个交点分别位于原点两侧,则a,b,c符号( )
| A、a<0,b<0,c<0 | B、a<0,b>0,c>0 | C、a<0,b<0,c>0 | D、a<0,b>0,c<0 |
分析:根据条件顶点在第一象限与X轴的两个交点分别位于原点两侧,作出函数的图象,再由开口方向确定a,再由对称轴确定b,再由与y轴的交点确定c.
解答: 解:如图所示:
解:如图所示:
∵开口向下,
所以a<0;
∵-
>0
∴b>0
∵f(0)=c
∴c>0
故选B.
 解:如图所示:
解:如图所示:∵开口向下,
所以a<0;
∵-
| b |
| 2a |
∴b>0
∵f(0)=c
∴c>0
故选B.
点评:本题主要考查二次函数作图,识图,用图的能力,把握二次函数的顶点,对称轴,开口方向是研究问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线y=ax2与直线y=kx+b(k≠0)交于A,B两点,且此两点的横坐标分别为x1,x2,直线与x轴的交点的横坐标是x3,则恒有( )
| A、x3=x1+x2 | B、x1x2=x1x3+x2x3 | C、x3+x1+x2=0 | D、x1x2+x1x3+x2x3=0 |
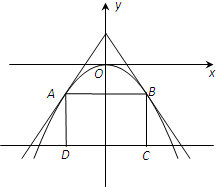 如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.
如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.