题目内容
若函数f(x)为定义域D上单调函数,且存在区间[a,b]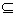 D(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的正函数,区间[a,b]叫做等域区间,
D(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的正函数,区间[a,b]叫做等域区间,
(1)已知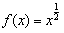 是[0,+∞)上的正函数,求f(x)的等域区间;
是[0,+∞)上的正函数,求f(x)的等域区间;
(2)试探究是否存在实数m,使得函数g(x)=x2+m是(-∞,0)上的正函数?若存在,请求出实数m的取值范围;若不存在,请说明理由。
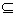 D(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的正函数,区间[a,b]叫做等域区间,
D(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的正函数,区间[a,b]叫做等域区间,(1)已知
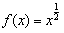 是[0,+∞)上的正函数,求f(x)的等域区间;
是[0,+∞)上的正函数,求f(x)的等域区间;(2)试探究是否存在实数m,使得函数g(x)=x2+m是(-∞,0)上的正函数?若存在,请求出实数m的取值范围;若不存在,请说明理由。
解:(1)因为 是[0,+∞)上的正函数,且
是[0,+∞)上的正函数,且 在[0,+∞)上单调递增,
在[0,+∞)上单调递增,
所以当x∈[a,b]时, ,
,
解得a=0,b=1,
故函数f(x)的“等域区间”为[0,1];
(2)因为函数 是(-∞,0)上的减函数,
是(-∞,0)上的减函数,
所以当x∈[a,b]时, ,
,
两式相减得 ,即b=-(a+1),
,即b=-(a+1),
代入 ,
,
由a<b<0,且b=-(a+1)得 ,
,
故关于a的方程 内有实数解,
内有实数解,
记 ,
,
则 ,解得
,解得 。
。
 是[0,+∞)上的正函数,且
是[0,+∞)上的正函数,且 在[0,+∞)上单调递增,
在[0,+∞)上单调递增,所以当x∈[a,b]时,
 ,
,解得a=0,b=1,
故函数f(x)的“等域区间”为[0,1];
(2)因为函数
 是(-∞,0)上的减函数,
是(-∞,0)上的减函数,所以当x∈[a,b]时,
 ,
,两式相减得
 ,即b=-(a+1),
,即b=-(a+1),代入
 ,
,由a<b<0,且b=-(a+1)得
 ,
,故关于a的方程
 内有实数解,
内有实数解,记
 ,
, 则
 ,解得
,解得 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 若函数f(x)为定义在R上的奇函数,且x∈(0,+∞)时,f(x)=2x
若函数f(x)为定义在R上的奇函数,且x∈(0,+∞)时,f(x)=2x