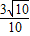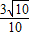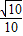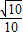题目内容
已知α是第二象限角,
(1)若cosα=-
,求sinα和tanα的值;(2)化简
•tanα
(1)若cosα=-
| 3 |
| 4 |
1-cos2(
|
分析:(1)若cosα=-
,则可通过同角三角函数的基本关系求出sinα和tanα的值,由于α是第二象限角故正弦为正,正切为负;
(2)通过诱导公式将
•tanα变形后再用三角函数的基本关系中的商数关系切化弦,化简
| 3 |
| 4 |
(2)通过诱导公式将
1-cos2(
|
解答:解:(1)∵α是第二象限角,
∴sinα>0,又∵cosα=-
,
∴sinα=
=
=
tanα=
=
=-
(2)
•tanα=
•tanα=-cosαtanα=-cosα×
=-sinα
∴sinα>0,又∵cosα=-
| 3 |
| 4 |
∴sinα=
| 1-cos2α |
1-
|
| ||
| 4 |
tanα=
| sinα |
| cosα |
| ||||
-
|
| ||
| 3 |
(2)
1-cos2(
|
| 1-sin2α |
| sinα |
| cosα |
点评:本题考查三角函数的化简求值以及诱导公式在化简中的应用,解题的关键是熟练掌握同角三角函数的关系及诱导公式,本题是基本概念与运算考查题,熟练掌握公式是顺利变形的基础.

练习册系列答案
相关题目

 是第二象限角,
是第二象限角, ,则
,则 = .
= .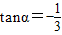 ,则cosα=( )
,则cosα=( )