题目内容
(本题满分12分)设椭圆C的中心在坐标原点O,焦点在x轴上,短轴长为![]() ,左焦点到左准线的距离为
,左焦点到左准线的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C上有不同两点P、Q,且OP⊥OQ,过P、Q的直线为l,求点O到直线l的距离.
解 (1)设椭圆C的方程为![]() (a>b>0),
(a>b>0),
则 ![]() ,
,![]() .
.
由 ![]() ,即
,即 ![]() ,得
,得 ![]() .
.
于是 a2 = b2 + c2 = 21 + 7 = 28,椭圆C的方程为![]() .………………… 5分
.………………… 5分
(2)若直线l的斜率不存在,即l⊥x轴时,不妨设l与x正半轴交于点M,将x = y代入![]() 中,得
中,得![]() ,则点P(
,则点P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),于是点O到l的距离为
),于是点O到l的距离为![]() . …………………… 7分
. …………………… 7分
若直线l的斜率存在,设l的方程为y = kx + m(k,m∈R),则点P(x1,y1),Q(x2,y2)的坐标是方程组 的两个实数解,
的两个实数解,
消去y,整理,得(3 + 4k2)x2 + 8kmx + 4m2-84 = 0,
∴ △ =(8km)2-4(3 + 4k2)(4m2-84)= 12(28k2-m2 + 21)>0, ①
![]() ,
,![]() . ②
. ②
…………………… 9分
∵ OP⊥OQ,∴ kOP · kOQ =-1,即 ![]() ,x1x2 + y1y2 = 0.
,x1x2 + y1y2 = 0.
于是 x1x2 +(kx1 + m)(kx2 + m)=(1 + k2)x1x2 + km(x1 + x2)+ m2 = 0. ③
将 x1 + x2,x1x2 代入上式,得 ![]() ,
,
∴(k2 + 1)(4m2-84)-8k2m2 + m2(4k2 + 3)= 0,
化简,得 m2 = 12(k2 + 1). ④
④代入①满足,因此原点O到直线l的距离 ![]() .
.
…………………… 12分

 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;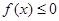 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求