题目内容
定义在R上的函数y=f(x),满足f(3-x)=f(x),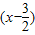 f′(x)<0,若x1<x2,且x1+x2>3则有( )
f′(x)<0,若x1<x2,且x1+x2>3则有( )A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.不确定
【答案】分析:由“f(3-x)=f(x)”,知函数图象关于直线x= 对称,再由“
对称,再由“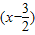 f′(x)<0”可知:当x>
f′(x)<0”可知:当x> 时,函数是减函数
时,函数是减函数
当x< 时,函数是增函数,最后由“x1<x2,且x1+x2>3”,得知x1,x2∈(
时,函数是增函数,最后由“x1<x2,且x1+x2>3”,得知x1,x2∈( ,+∞),应用单调性定义得到结论.
,+∞),应用单调性定义得到结论.
解答:解:∵f(3-x)=f(x),
∴函数图象关于直线x= 对称,
对称,
又∵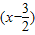 f′(x)<0
f′(x)<0
∴当x> 时,函数是减函数
时,函数是减函数
当x< 时,函数是增函数
时,函数是增函数
∵x1<x2,且x1+x2>3
∴x1,x2∈( ,+∞)
,+∞)
∴f(x1)>f(x2)
故选B
点评:本题主要考查函数的对称性和单调性,这里还考查了导数,当导数大于零时,函数是增函数,当导数小于零时,函数是减函数.
 对称,再由“
对称,再由“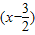 f′(x)<0”可知:当x>
f′(x)<0”可知:当x> 时,函数是减函数
时,函数是减函数当x<
 时,函数是增函数,最后由“x1<x2,且x1+x2>3”,得知x1,x2∈(
时,函数是增函数,最后由“x1<x2,且x1+x2>3”,得知x1,x2∈( ,+∞),应用单调性定义得到结论.
,+∞),应用单调性定义得到结论.解答:解:∵f(3-x)=f(x),
∴函数图象关于直线x=
 对称,
对称,又∵
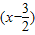 f′(x)<0
f′(x)<0∴当x>
 时,函数是减函数
时,函数是减函数当x<
 时,函数是增函数
时,函数是增函数∵x1<x2,且x1+x2>3
∴x1,x2∈(
 ,+∞)
,+∞)∴f(x1)>f(x2)
故选B
点评:本题主要考查函数的对称性和单调性,这里还考查了导数,当导数大于零时,函数是增函数,当导数小于零时,函数是减函数.

练习册系列答案
相关题目