题目内容
已知函数f(x)是定义域R的奇函数,给出下列6个函数:
(1)g(x)=3• ;
;
(2)g(x)=x+1;
(3) ;
;
(4) ;
;
(5)g(x)= ;
;
(6) .
.
其中可以使函数F(x)=f(x)•g(x)是偶函数的函数序号是________.
解:∵函数f(x)是定义域R的奇函数,F(x)=f(x)•g(x)是偶函数
∴函数g(x)是定义域R的奇函数
(1)定义域为R,g(-x)=3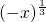 =-3•
=-3• =-g(x),是奇函数
=-g(x),是奇函数
(2)定义域为R,g(-x)=-x+1≠-x-1=-g(x),不是奇函数
(3)定义域为R, =cosx,g(-x)=cos(-x)=cosx=g(x),是偶函数
=cosx,g(-x)=cos(-x)=cosx=g(x),是偶函数
(4)定义域为R, ,是奇函数
,是奇函数
(5)g(x)= 的定义域为{x|x≠
的定义域为{x|x≠ }不关于原点对称,故非奇非偶函数
}不关于原点对称,故非奇非偶函数
(6)定义域为R, ,
, ,是奇函数.
,是奇函数.
故答案为:(1)(4)(6)
分析:根据函数f(x)是定义域R的奇函数,F(x)=f(x)•g(x)是偶函数可知函数g(x)是奇函数,然后根据奇函数的定义进行一一判定即可.
点评:本题主要考查了函数奇偶性的判断,一般步骤先判定定义域是否关于原点对称,然后判定f(-x)与f(x)的关系,属于中档题.
∴函数g(x)是定义域R的奇函数
(1)定义域为R,g(-x)=3
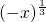 =-3•
=-3• =-g(x),是奇函数
=-g(x),是奇函数(2)定义域为R,g(-x)=-x+1≠-x-1=-g(x),不是奇函数
(3)定义域为R,
 =cosx,g(-x)=cos(-x)=cosx=g(x),是偶函数
=cosx,g(-x)=cos(-x)=cosx=g(x),是偶函数(4)定义域为R,
 ,是奇函数
,是奇函数(5)g(x)=
 的定义域为{x|x≠
的定义域为{x|x≠ }不关于原点对称,故非奇非偶函数
}不关于原点对称,故非奇非偶函数(6)定义域为R,
 ,
, ,是奇函数.
,是奇函数.故答案为:(1)(4)(6)
分析:根据函数f(x)是定义域R的奇函数,F(x)=f(x)•g(x)是偶函数可知函数g(x)是奇函数,然后根据奇函数的定义进行一一判定即可.
点评:本题主要考查了函数奇偶性的判断,一般步骤先判定定义域是否关于原点对称,然后判定f(-x)与f(x)的关系,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+