题目内容
已知函数y=f(x),若存在x0,使得f(x0)=x0,则x0称是函数y=f(x)的一个不动点,设 .
.
(1)求函数y=f(x)的不动点;
(2)对(1)中的二个不动点a、b(假设a>b),求使 恒成立的常数k的值;
恒成立的常数k的值;
(3)对由a1=1,an=f(an-1)定义的数列{an},求其通项公式an.
解:(1)设函数y=f(x)的一个不动点为x0,
则
(2)由(1)可知
可知使 恒成立的常数k=8.
恒成立的常数k=8.
(3)由(2)知
可知数列 为首项,8为公比的等比数列
为首项,8为公比的等比数列
即以 为首项,8为公比的等比数列.则
为首项,8为公比的等比数列.则
∴ .
.
分析:(1)设函数y=f(x)的一个不动点为x0,然后根据不动点的定义建立方程,解之即可;
(2)由(1)可知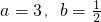 ,代入
,代入 可求出常数k的值;
可求出常数k的值;
(3)由(2)可知数列 为首项,8为公比的等比数列,然后求出通项,即可求出数列{an}的 通项公式.
为首项,8为公比的等比数列,然后求出通项,即可求出数列{an}的 通项公式.
点评:本题主要考查了函数恒成立问题,以及等比数列求通项,同时考查了前后问题之间的联系,属于中档题.
则

(2)由(1)可知

可知使
 恒成立的常数k=8.
恒成立的常数k=8.(3)由(2)知

可知数列
 为首项,8为公比的等比数列
为首项,8为公比的等比数列即以
 为首项,8为公比的等比数列.则
为首项,8为公比的等比数列.则
∴
 .
.分析:(1)设函数y=f(x)的一个不动点为x0,然后根据不动点的定义建立方程,解之即可;
(2)由(1)可知
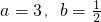 ,代入
,代入 可求出常数k的值;
可求出常数k的值;(3)由(2)可知数列
 为首项,8为公比的等比数列,然后求出通项,即可求出数列{an}的 通项公式.
为首项,8为公比的等比数列,然后求出通项,即可求出数列{an}的 通项公式.点评:本题主要考查了函数恒成立问题,以及等比数列求通项,同时考查了前后问题之间的联系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足