题目内容
已知椭圆短轴端点、焦点及中心连线构成等腰直角三角形,则此椭圆的离心率=分析:由题意椭圆短轴端点、焦点及中心连线构成等腰直角三角形,可得出b=c,结合a2=b2+c2,求出离心率
解答:解:由题意椭圆短轴端点、焦点及中心连线构成等腰直角三角形,可得出b=c,
又a2=b2+c2,故有a2=2c2,解得
=
即e=
故答案为:
.
又a2=b2+c2,故有a2=2c2,解得
| c |
| a |
| ||
| 2 |
即e=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查椭圆的简单性质,解题的关键是根据题设条件得出a,b,c三个量之间的关系,由此关系求出椭圆的离心率.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
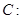
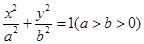 的离心率为
的离心率为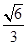 ,椭圆短轴的一个端点与两个焦
,椭圆短轴的一个端点与两个焦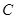 的方程;
的方程;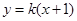 与椭圆
与椭圆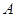 、
、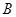 两点. ①若线段
两点. ①若线段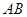 中点的
中点的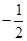 ,求斜率
,求斜率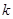 的值;②若点
的值;②若点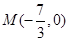 ,求证:
,求证: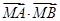 为定值.
为定值.