题目内容
下列命题正确的是
- A.函数
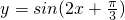 在区间
在区间 内单调递增
内单调递增 - B.函数y=cos4x-sin4x的最小正周期为2π
- C.函数
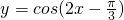 的图象是关于直线
的图象是关于直线 成轴对称的图形
成轴对称的图形 - D.函数
 的图象是关于点
的图象是关于点 成中心对称的图形
成中心对称的图形
C
分析:A:要求正弦型函数单调增区间,直接将区间代入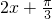 ,看成整体的取值是否为正弦函数的单调增区间即可;
,看成整体的取值是否为正弦函数的单调增区间即可;
B:利用三角关系式将函数化简为一个正弦或余弦函数;
C:将 代入函数看函数值是否取得最值;D:将
代入函数看函数值是否取得最值;D:将 代入函数看函数值是否为0.
代入函数看函数值是否为0.
解答:∵ ∴
∴ ,而y=sint在
,而y=sint在 上递增.故A不正确.
上递增.故A不正确.
∵y=cos4x-sin4x=cos2x-sin2x=cos2x,∴其最小正周期是π.故B也不正确.
∵x= 时,
时, ,
, ∴C正确.
∴C正确.
∵ ,∴D也不正确.
,∴D也不正确.
故选C
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数的一些性质,我们可以根据三角函数的性质对四个结论逐一进行判断,可以得到正确的结论.
分析:A:要求正弦型函数单调增区间,直接将区间代入
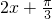 ,看成整体的取值是否为正弦函数的单调增区间即可;
,看成整体的取值是否为正弦函数的单调增区间即可;B:利用三角关系式将函数化简为一个正弦或余弦函数;
C:将
 代入函数看函数值是否取得最值;D:将
代入函数看函数值是否取得最值;D:将 代入函数看函数值是否为0.
代入函数看函数值是否为0.解答:∵
 ∴
∴ ,而y=sint在
,而y=sint在 上递增.故A不正确.
上递增.故A不正确.∵y=cos4x-sin4x=cos2x-sin2x=cos2x,∴其最小正周期是π.故B也不正确.
∵x=
 时,
时, ,
, ∴C正确.
∴C正确.∵
 ,∴D也不正确.
,∴D也不正确.故选C
点评:本题考查的知识点是,判断命题真假,比较综合的考查了三角函数的一些性质,我们可以根据三角函数的性质对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
相关题目
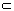 平面β,则下列命题正确的是
平面β,则下列命题正确的是  ,直线b
,直线b 直线a,b
直线a,b 平面
平面 ,则
,则
 则
则 B.若
B.若 , 则
, 则
 则
则 D.若
D.若