题目内容
命题P：?α∈R，sin（π-α）=cosα；
命题q：?m＞0，双曲线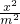
-
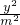=1的离心率为
．
则下面结论正确的是
- A.P是假命题
- B.￢q是真命题
- C.p∧q是假命题
- D.p∨q是真命题
D
分析：由于可判断命题p为真命题，而命题q为真命题，再根据复合命题的真假判定，一一验证选项即可得正确结果．
解答：当
时，Rsin（π-α）=cosα，故命题p为真命题，
∵双曲线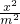-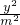=1中a=b=|m|=m，
∴c=
=m
∴e=
=，故命题q为真命题．
∴￢p为假命题，￢q是假命题，p∨q是真命题；
故选D．
点评：本题主要考查了命题真假判断的应用，简单复合命题的真假判断，属于基础试题．
分析：由于可判断命题p为真命题，而命题q为真命题，再根据复合命题的真假判定，一一验证选项即可得正确结果．
解答：当
时，Rsin（π-α）=cosα，故命题p为真命题，∵双曲线
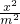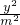-=1中a=b=|m|=m，∴c=
=m∴e=
=，故命题q为真命题．∴￢p为假命题，￢q是假命题，p∨q是真命题；
故选D．
点评：本题主要考查了命题真假判断的应用，简单复合命题的真假判断，属于基础试题．
练习册系列答案
相关题目
），
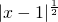．则以下四个命题对已知的三个函数都能成立的是
）
； 
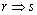B．p：
q：
q： 
D． p：
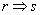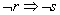
q：