题目内容
在△ABC中,若 ,则△ABC是( )
,则△ABC是( )A.等边三角形
B.锐角三角形
C.钝角三角形
D.直角三角形
【答案】分析:由题意可知向量 与
与 的夹角为A,记|
的夹角为A,记| |=c,|
|=c,| |=b,|
|=b,| |=a,cosA=
|=a,cosA= ,又由余弦定理可得cosA=
,又由余弦定理可得cosA= ,化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形,即得答案.
,化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形,即得答案.
解答:解:由题意可知向量 与
与 的夹角为A,记|
的夹角为A,记| |=c,|
|=c,| |=b,|
|=b,| |=a
|=a
则由 可得,c2=bc•cosA+a2,即cosA=
可得,c2=bc•cosA+a2,即cosA=
又由余弦定理可得cosA= ,故
,故 =
=
化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形.
故选D.
点评:本题为三角形形状的判断,化简向量式和利用余弦定理是解决问题的关键,属中档题.
 与
与 的夹角为A,记|
的夹角为A,记| |=c,|
|=c,| |=b,|
|=b,| |=a,cosA=
|=a,cosA= ,又由余弦定理可得cosA=
,又由余弦定理可得cosA= ,化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形,即得答案.
,化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形,即得答案.解答:解:由题意可知向量
 与
与 的夹角为A,记|
的夹角为A,记| |=c,|
|=c,| |=b,|
|=b,| |=a
|=a则由
 可得,c2=bc•cosA+a2,即cosA=
可得,c2=bc•cosA+a2,即cosA=
又由余弦定理可得cosA=
 ,故
,故 =
=
化简可得c2=a2+b2,由勾股定理可知△ABC为直角三角形.
故选D.
点评:本题为三角形形状的判断,化简向量式和利用余弦定理是解决问题的关键,属中档题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 ,则B的值为( )
,则B的值为( )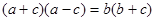 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.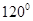 D.
D.
 ,则∠A=
,则∠A= 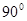 B.
B.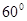 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2