题目内容
已知双曲线 的焦点与椭圆
的焦点与椭圆 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为 ,
, 是椭圆上的的动点.
是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: ,直线
,直线 与
与 的斜率之积为
的斜率之积为 ,求证:存在定点
,求证:存在定点 ,
,
使得 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若 在第一象限,且点
在第一象限,且点 关于原点对称,点
关于原点对称,点 在
在 轴的射影为
轴的射影为 ,连接
,连接 并延长交椭圆于
并延长交椭圆于
点 ,求证:以
,求证:以 为直径的圆经过点
为直径的圆经过点 .
.
(1)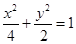 ;(2)存在
;(2)存在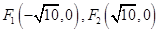 ;(3)证明过程详见试题解析.
;(3)证明过程详见试题解析.
解析试题分析:(1)由双曲线 的焦点与椭圆
的焦点与椭圆 的焦点重合求出椭圆中的
的焦点重合求出椭圆中的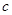 ,再由
,再由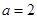 ,求出所求椭圆方程为
,求出所求椭圆方程为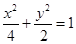 ;(2)先设
;(2)先设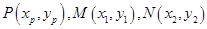 ,由
,由 ,结合椭圆的标准方程可以得到
,结合椭圆的标准方程可以得到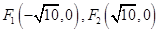 使得
使得 为定值;(3)要证明以
为定值;(3)要证明以 为直径的圆经过点
为直径的圆经过点 ,就是证明
,就是证明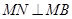 ,详见解析.
,详见解析.
试题解析:(1)解:由题设可知:双曲线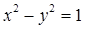 的焦点为
的焦点为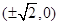 ,
,
所以椭圆中的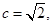
又由椭圆的长轴为4得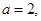
故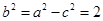
故椭圆的标准方程为: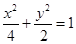
(2)证明:设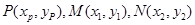 ,由
,由 可得:
可得: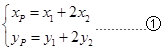
由直线 与
与 的斜率之积为
的斜率之积为 可得:
可得: ,即
,即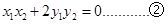
由①②可得: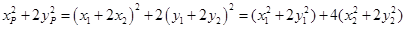 …6分
…6分
M、N是椭圆上,故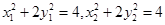
故 ,即
,即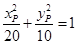
由椭圆定义可知存在两个定点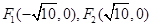 ,使得动点P到两定点距离和为定值
,使得动点P到两定点距离和为定值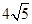 ;
;
(3)证明:设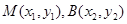
由题设可知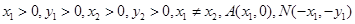
由题设可知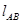 斜率存在且满足
斜率存在且满足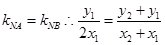 .……③
.……③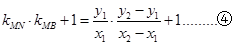
将③代入④可得: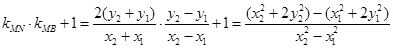 …⑤
…⑤
点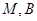 在椭圆
在椭圆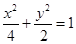 ,故
,故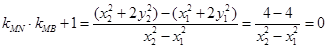
所以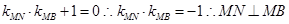
因此以 为直径的圆经过点
为直径的圆经过点 .
.
考点:直线与圆锥曲线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
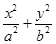 =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.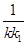 +
+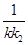 为定值,并求出这个定值.
为定值,并求出这个定值. =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0). ,求双曲线的离心率.
,求双曲线的离心率.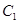 、抛物线
、抛物线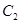 的焦点均在
的焦点均在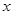 轴上,
轴上,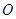 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: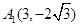 、
、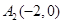 、
、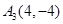 、
、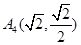 .
.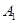 ,
,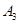 在抛物线
在抛物线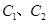 的标准方程;
的标准方程; 的坐标并求出椭圆
的坐标并求出椭圆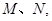 且满足
且满足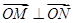 ,试求出直线的方程.
,试求出直线的方程.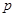 :方程
:方程 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆;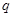 :双曲线
:双曲线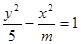 的离心率
的离心率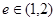 ,若
,若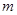 的取值范围.
的取值范围. =1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x-
=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x- 的距离为
的距离为 -
- ,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
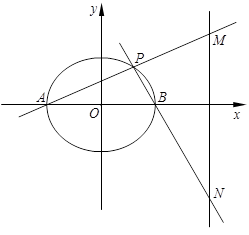
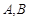 分别是椭圆
分别是椭圆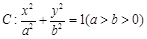 的左,右顶点,点
的左,右顶点,点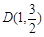 在椭圆
在椭圆 上,且直线
上,且直线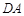 与直线
与直线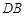 的斜率之积为
的斜率之积为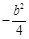 .
.
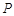 为椭圆
为椭圆 ,
,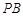 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点 ,
,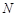 .
.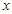 轴上是否存在一个定点
轴上是否存在一个定点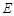 ,使得
,使得 ?若存在,求点
?若存在,求点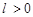 ,求
,求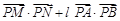 的取值范围.
的取值范围.