题目内容
设数列![]() 的前
的前![]() 项的和
项的和![]() ,
,![]()
(Ⅰ)求首项![]() 与通项
与通项![]() ;
;
(Ⅱ)设![]() ,
,![]() ,证明:
,证明:![]() .
.
(Ⅰ)a1=2,an=4n-2n, n=1,2,3, …,;(Ⅱ)同解析;
解析:
(Ⅰ)由 Sn=an-×2n+1+, n=1,2,3,… , ①
得 a1=S1= a1-×4+ 所以a1=2.
再由①有 Sn-1=an-1-×2n+, n=2,3,4,…
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n),n=2,3, …
整理得: an+2n=4(an-1+2n-1),n=2,3, … ,
因而数列{ an+2n}是首项为a1+2=4,公比为4的等比数列,
即 : an+2n=4×4n-1= 4n, n=1,2,3, …,
因而an=4n-2n, n=1,2,3, …,
(Ⅱ)将an=4n-2n代入①得:
Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×( - )
所以, ![]() =
= ![]() - )
- )
= ×( - ) <

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
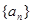 的前项和为
的前项和为 ,已知
,已知 (
( ).
).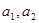 的值;
的值; 是等比数列;
是等比数列; 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列 ,若
,若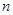 项的和为
项的和为 ,求证:
,求证: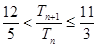 .
. 中,
中, [来源:]
[来源:] 为等比数列;
为等比数列; 项的和为
项的和为 ,若
,若 ,求:正整数
,求:正整数 的前
的前 项的和为
项的和为 ,且
,且
 ,
,
 是等比数列,并求通项
是等比数列,并求通项 ;
; ,
, ,证明:
,证明: