题目内容
已知直线 (a>0,b>0)过点(1,4),则a+b最小值是
(a>0,b>0)过点(1,4),则a+b最小值是
- A.16
- B.9
- C.8
- D.3
B
分析:将点的坐标代入直线方程得到 (a>0,b>0),得到a+b=
(a>0,b>0),得到a+b= ,展开后利用基本不等式求出函数的最小值.
,展开后利用基本不等式求出函数的最小值.
解答:因为直线 (a>0,b>0)过点(1,4),
(a>0,b>0)过点(1,4),
所以 (a>0,b>0),
(a>0,b>0),
所以a+b=
 ,
,
当且仅当 取等号,
取等号,
所以a+b最小值是9,
故选B.
点评:本题考查利用基本不等式求函数的最值,一定要注意使用的条件:一正、二定、三相等,属于基础题.
分析:将点的坐标代入直线方程得到
 (a>0,b>0),得到a+b=
(a>0,b>0),得到a+b= ,展开后利用基本不等式求出函数的最小值.
,展开后利用基本不等式求出函数的最小值.解答:因为直线
 (a>0,b>0)过点(1,4),
(a>0,b>0)过点(1,4),所以
 (a>0,b>0),
(a>0,b>0),所以a+b=

 ,
,当且仅当
 取等号,
取等号,所以a+b最小值是9,
故选B.
点评:本题考查利用基本不等式求函数的最值,一定要注意使用的条件:一正、二定、三相等,属于基础题.

练习册系列答案
相关题目
 (a>0,b>0)的上、下顶点分别为A、B,一个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列.
(a>0,b>0)的上、下顶点分别为A、B,一个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列. ,求△MBN的面积.
,求△MBN的面积.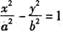 (a>0,b>0)的右焦点为F,过F且斜率为
(a>0,b>0)的右焦点为F,过F且斜率为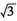 的直线交C于A、B两点,若
的直线交C于A、B两点,若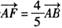 ,则C的离心率为( )
,则C的离心率为( )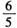 B.
B.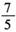 C.
C.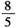 D.
D.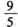
 (a>0,b>0)过点(1,4),则a+b最小值是( )
(a>0,b>0)过点(1,4),则a+b最小值是( )