Question

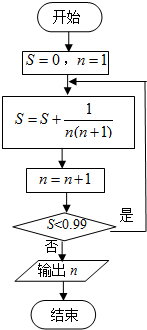阅读右面的程序框图，则输出的n的值为（　　）

A．98

B．99

C．100

D．101

Answer 1

分析：先根据判断框中的条件可知该循环体执行的次数，然后根据循环体建立等式，利用裂项求和法求出即可．

解答：解：根据判断框中的条件可知该循环体执行n+1次
故计算S=0+

1

2×1

+…

1

(n+1)n

+

1

(n+2)(n+1)

=1 -

1

2

+

1

2

-

1

3

+…+

1

n+1

-

1

n+2

=

n+1

n+2

由

n+1

n+2

＜0.99⇒n＞98．
则输出的n的值为99
故选B．

点评：本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，解题的关键是判定出循环的次数，属于基础题．