题目内容
已知f(x)=ax2+bx+c的图象过点(-1,0),是否存在常数a、b、c,使不等式
思路分析:此题是函数、不等式、命题的综合题,首先判断是全称命题还是特称命题,若是全称命题,可以利用特殊值,然后利用一元二次不等式恒成立的条件,来解不等式组即可解决问题.
解:∵f(x)的图象过点(-1,0),∴a-b+c=0.
∵x≤f(x)≤![]() 对一切x∈R均成立,
对一切x∈R均成立,
∴当x=1时也成立,即1≤a+b+c≤1,
故有a+b+c=1.
∴b=![]() ,c=
,c=![]() .
.
∴f(x)=ax2+![]() -a,故应x≤ax2+
-a,故应x≤ax2+![]() 对一切x∈R成立,
对一切x∈R成立,
即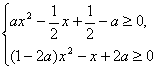 恒成立
恒成立![]()
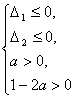
![]()
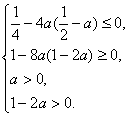
∴a=![]() .∴c=
.∴c=![]() .
.
∴存在一组常数:a=![]() ,b=
,b=![]() ,c=
,c=![]() ,
,
使不等式x≤f(x)≤![]() 对一切实数x均成立.
对一切实数x均成立.

练习册系列答案
相关题目