题目内容
三棱锥P-ABC中,PA,PB,PC两两垂直,如果此三棱锥外接球的表面积为9π,那么PA•PB+PA•PC+PB•PC的最大值为( )
A、
| ||
B、
| ||
| C、9 | ||
| D、18 |
分析:三棱锥的三条侧棱两两垂直,扩展为长方体,二者的外接球是同一个,根据球的表面积,求出球的直径,就是长方体的对角线长,设出三度,利用基本不等式求出表达式的最值.
解答:解:三棱锥的三条侧棱两两垂直,扩展为长方体,二者的外接球是同一个,因为三棱锥外接球的表面积为9π,
所以球的半径为:r=
,球的直径为:3
设长方体的三度为:a,b,c,所以a2+b2+c2=9
PA•PB+PA•PC+PB•PC=ab+bc+ac≤a2+b2+c2=9,当且仅当a=b=c时取等号.
故选C
所以球的半径为:r=
| 3 |
| 2 |
设长方体的三度为:a,b,c,所以a2+b2+c2=9
PA•PB+PA•PC+PB•PC=ab+bc+ac≤a2+b2+c2=9,当且仅当a=b=c时取等号.
故选C
点评:本题是基础题,考查球的内接体知识,基本不等式的应用,考查空间想象能力,计算能力,三棱锥扩展为长方体是本题的关键.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.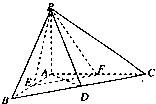 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,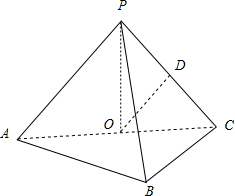 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.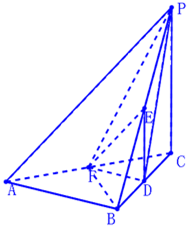 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.