题目内容
已知数列{an}的各项均为正整数,其前n项和为Sn.若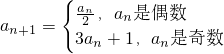 且S3=29,则a1=________;S3n=________.
且S3=29,则a1=________;S3n=________.
5 7n+22
分析:通过对a1分4k,4k+1,4k+2,4k+3(k∈N*)讨论,及与已知条件,结合S3=29,即可求出a1;通过求出a1,a2,…,a9,知道:从a4开始数列{an}是一个周期为3的数列,进而即可得到S3n.
解答:(1)①若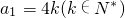 ,则a2=2k,a3=k,∴S3=a1+a2+a3=7k=29,
,则a2=2k,a3=k,∴S3=a1+a2+a3=7k=29,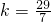 不是整数,舍去;
不是整数,舍去;
②若a1=4k+1,则a2=3(4k+1)+1=12k+4,a3=6k+2,∴S3=a1+a2+a3=22k+7=29,解得k=1,∴a1=5.
③若a1=4k+2,则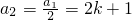 ,a3=3a2+1=3(2k+1)+1=6k+4,则S3=a1+a2+a3=12k+7=29,解得k=
,a3=3a2+1=3(2k+1)+1=6k+4,则S3=a1+a2+a3=12k+7=29,解得k= ,应舍去;
,应舍去;
④若a1=4k+3,则a2=3(4k+3)+1=12k+10,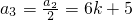 ,则S3=a1+a2+a3=22k+18=29,解得k=
,则S3=a1+a2+a3=22k+18=29,解得k= 不是整数,舍去.
不是整数,舍去.
综上可得:a1=5
(2)∵a1=5,a2=16,a3=8,∴a4=4,a5=2,a6=1,a7=4,a8=2,a9=1….
可以看到:从a4开始数列{an}是一个周期为3的数列,即an+3=an,(n≥4).
因此,当n≥2时,S3n=29+7(n-1)=7n+22,当n=1时,上式也成立,故S3n=7n+22.
点评:数列掌握分类讨论的思想方法和数列的周期性是解题的关键.
分析:通过对a1分4k,4k+1,4k+2,4k+3(k∈N*)讨论,及与已知条件,结合S3=29,即可求出a1;通过求出a1,a2,…,a9,知道:从a4开始数列{an}是一个周期为3的数列,进而即可得到S3n.
解答:(1)①若
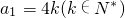 ,则a2=2k,a3=k,∴S3=a1+a2+a3=7k=29,
,则a2=2k,a3=k,∴S3=a1+a2+a3=7k=29,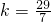 不是整数,舍去;
不是整数,舍去;②若a1=4k+1,则a2=3(4k+1)+1=12k+4,a3=6k+2,∴S3=a1+a2+a3=22k+7=29,解得k=1,∴a1=5.
③若a1=4k+2,则
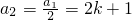 ,a3=3a2+1=3(2k+1)+1=6k+4,则S3=a1+a2+a3=12k+7=29,解得k=
,a3=3a2+1=3(2k+1)+1=6k+4,则S3=a1+a2+a3=12k+7=29,解得k= ,应舍去;
,应舍去;④若a1=4k+3,则a2=3(4k+3)+1=12k+10,
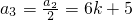 ,则S3=a1+a2+a3=22k+18=29,解得k=
,则S3=a1+a2+a3=22k+18=29,解得k= 不是整数,舍去.
不是整数,舍去.综上可得:a1=5
(2)∵a1=5,a2=16,a3=8,∴a4=4,a5=2,a6=1,a7=4,a8=2,a9=1….
可以看到:从a4开始数列{an}是一个周期为3的数列,即an+3=an,(n≥4).
因此,当n≥2时,S3n=29+7(n-1)=7n+22,当n=1时,上式也成立,故S3n=7n+22.
点评:数列掌握分类讨论的思想方法和数列的周期性是解题的关键.

练习册系列答案
相关题目
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)