题目内容
(本小题满分12分)如图,在四棱锥O―ABCD中,底面ABCD是边长为1的菱形,![]() ,OA⊥底面ABCD, OA = 2,M为OA的中点。
,OA⊥底面ABCD, OA = 2,M为OA的中点。
(Ⅰ)求异面直线AB与MD所成角的大小;
(Ⅱ)求点B到面OCD的距离。
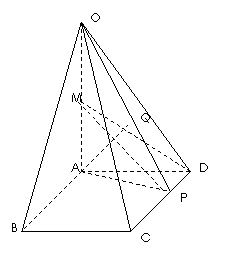
本小题主要考查直线与直线、直线与平面的位置关系、异面直线所成角及点到平面的距离等知识,考查空间想象能力和思维能力,用综合法或向量法解决立体几何问题的能力。
解:方法一(综合法)
(Ⅰ)∵CD∥AB,
∴∠MDC为异面直线AB与MD所成角(或其补角)
作AP⊥CD于点P,连接MP
∵OA⊥底面ABCD,∴CD⊥MP。
∵![]() , ∴
, ∴![]()
∵![]()
∴![]()
∴AB与MD所成角的大小为![]() 。
。
(Ⅱ)∵AB∥平面OCD,∴点B和点A到平面OCD的距离相等
连接OP,过点A作AQ⊥OP与点Q,
∵AP⊥CD,OA⊥CD,∴CD⊥平面OAP
∵![]() 平面OAP,∴
平面OAP,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面O CD,线段
平面O CD,线段![]() 的长就是点A到平面OCD的距离。
的长就是点A到平面OCD的距离。
∵![]() ,
,![]()
∴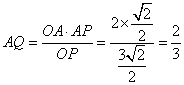 ,∴点B到面OCD的距离为
,∴点B到面OCD的距离为![]() 。
。
方法二(向量法):
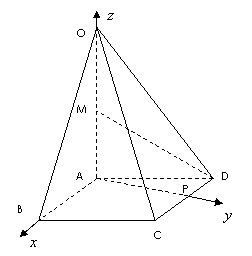
作AP⊥CD与点P。如图,分别以AB,AP,AO所在直线为
![]() 轴建立直角坐标系。
轴建立直角坐标系。
![]()
![]()
(Ⅰ)设AB与MD所成角为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴AB与MD所成角的大小为
,∴AB与MD所成角的大小为![]() 。
。
(Ⅱ)![]()
设平面OCD的法向量为![]() ,则
,则![]() ,
,
得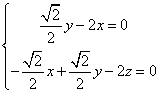 ,取
,取![]() ,解得
,解得![]() 。
。
设点B到面OCD的距离为![]() ,则
,则![]() 为
为![]() 在向量
在向量![]() 上的投影的绝对值。
上的投影的绝对值。
∵![]() ,∴
,∴![]()
∴点B到面OCD的距离为![]() 。
。

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目