题目内容
已知定义在 上的单调函数
上的单调函数 满足:存在实数
满足:存在实数 ,使得对于任意实数
,使得对于任意实数 ,总有
,总有 恒成立,则(i)
恒成立,则(i) (ii)
(ii) 的值为
的值为
0;1
解析试题分析:由题意对于任意实数x1,x2等式恒成立,故可采用赋值法求解.
(i)令 ,则f(
,则f( )=f(
)=f( )+f(1)+f(0),故f(1)+f(0)=0;
)+f(1)+f(0),故f(1)+f(0)=0;
(ii)令 则f(0)=f(
则f(0)=f( )+2f(0)所以f(x0)=-f(0)由(i)知f(1)=-f(0)=f(x0)又f(x)为单调函数,所以x0=1故答案为:0,1
)+2f(0)所以f(x0)=-f(0)由(i)知f(1)=-f(0)=f(x0)又f(x)为单调函数,所以x0=1故答案为:0,1
考点:抽象函数
点评:本题考查抽象函数的求值问题,一般采用赋值法解决.综合性较强.

练习册系列答案
相关题目
 则函数
则函数 的零点个数为 .
的零点个数为 . 的反函数
的反函数 .
.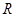 上的函数
上的函数 满足以下条件:
满足以下条件: (2)对任意
(2)对任意 .
. ;②
;② ;③
;③ ;④
;④ .其中一定成立的是 (请写出所有正确的序号)
.其中一定成立的是 (请写出所有正确的序号) ,
, 有下面四个结论:
有下面四个结论:
 是奇函数; (2)
是奇函数; (2) 恒成立;
恒成立; 的最大值是
的最大值是 ; (4)
; (4)  .
. 则f(f(-4))=______。
则f(f(-4))=______。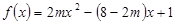 ,
, ,对
,对 R,
R, 与
与 的值至少有一个为正数,则
的值至少有一个为正数,则 的取值范围是 .
的取值范围是 .  ,定义运算“
,定义运算“ ”、“
”、“ ”为:
”为:
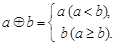
 ,②
,② ,
, , ④
, ④ .
.