题目内容
满足
的复数
的共轭复数是（ ）
A． | B． | C． | D． |
D
解析试题分析：由题意可得
，所以
解法二：得式两边都乘以
，可得，从而得．
考点：复数的基本概念，复数的基本运算．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
为虚数单位，则
A． | B． | C． | D． |
已知复数
在复平面内对应的点分别为
，则
等于（ ）
A． | B． | C． | D． |
若复数
（
为虚数单位）是纯虚数，则实数
的值为 （ ）
A． | B． | C． | D． |
如果复数
为纯虚数,则实数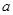
的值 ( )
| A．等于1 | B．等于2 | C．等于1或2 | D．不存在 |
设
是虚数单位，则“x=－3”是“复数z=（x2+2x－3）+（x－1）i为纯虚数”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
若复数z满足iz＝2＋4i，则在复平面内z对应的点的坐标是 ( )
| A．（2，4） | B．（2，－4） | C．（4，－2） | D．（4，2） |
设复数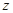
满足
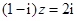，则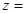
（ ）
A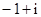． | B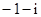． | C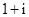． | D． |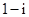
复数z=1-i,则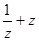
对应的点所在的象限为( )
| A．第一象限 | B．第二象限 | C．第三象跟 | D．第四象限 |