题目内容
设函数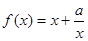 定义域为
定义域为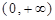 ,且
,且 .
.
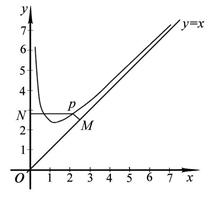
设点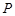 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点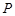 分别作直线
分别作直线 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.
(1)写出 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)
(2)问: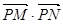 是否为定值?若是,则求出该定值,若不是,则说明理由;(7分)
是否为定值?若是,则求出该定值,若不是,则说明理由;(7分)
(3)设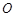 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.(7分)
面积的最小值.(7分)
(1) 在
在 上是减函数.(2)
上是减函数.(2) ;
;
(3)此时四边形 面积有最小值
面积有最小值 .
.
解析试题分析:(1)、因为函数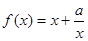 的图象过点
的图象过点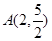 ,
,
所以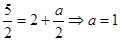 2分
2分
函数 在
在 上是减函数. 4分
上是减函数. 4分
(2)、(理)设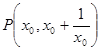 5分
5分
直线 的斜率
的斜率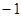
则 的方程
的方程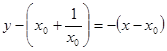 6分
6分
联立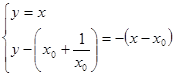
 9分
9分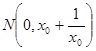
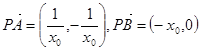 ,
,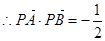 11分
11分
(3) 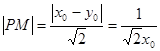 12分
12分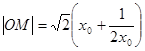 13分
13分
∴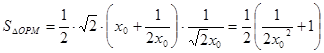 , 14分
, 14分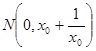
 , 15分
, 15分
∴  , 16分
, 16分 17分
17分
当且仅当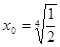 时,等号成立.
时,等号成立.
∴此时四边形 面积有最小值
面积有最小值 . 18分
. 18分
考点:本题主要考查函数的性质,均值定理的应用,向量的坐标运算。
点评:综合题,利用函数方程思想,得出面积表达式,进一步运用均值定理求面积的最小值,对数学式子变形能力要求较高。

 。
。 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数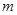 的取值范围。
的取值范围。 为奇函数,当
为奇函数,当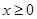 时,
时, (如图).
(如图).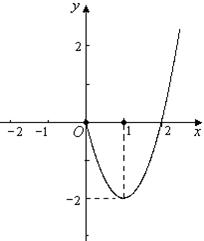
 在区间
在区间 上单调递增.
上单调递增.
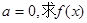 的单调区间;
的单调区间; 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于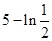 ,求a的取值范围。
,求a的取值范围。 ,设其定义域域是
,设其定义域域是 .
.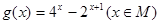 的值域.
的值域.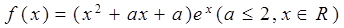
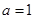 ,求函数
,求函数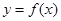 在点(0,
在点(0,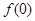 )处的切线方程;
)处的切线方程;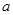 ,使得
,使得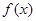 的极大值为3.若存在,求出
的极大值为3.若存在,求出 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为
,容积为 .
.
 是定义在
是定义在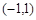 上的奇函数,当
上的奇函数,当 时
时 且
且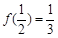 。
。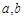 的值;
的值;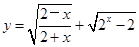 的定义域为
的定义域为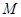 ,
,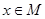 时,求函数
时,求函数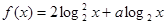 的最大值。
的最大值。