题目内容
已知函数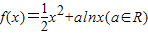 .
.(1)若a=-1,求f(x)的单调递增区间;
(2)当x>1时,f(x)>lnx恒成立,求实数a的取值范围.
【答案】分析:(1)若a=-1时,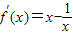 ,x>0,由f′(x)>0,能求出函数f(x)的单调递增区间.
,x>0,由f′(x)>0,能求出函数f(x)的单调递增区间.
(2)依题意得f(x)-lnx>0,故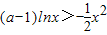 ,所以
,所以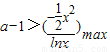 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.
解答:解:(1)∵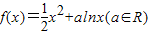 ,
,
∴若a=-1时,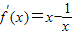 ,x>0,
,x>0,
由f′(x)>0,得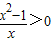 ,又x>0,解得x>1,
,又x>0,解得x>1,
所以函数f(x)的单调递增区间为(1,+∞).
(2)依题意得f(x)-lnx>0,
即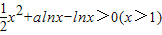 ,
,
∴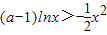
∵x>1,∴lnx>0
∴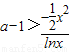 ,
,
∴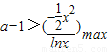 ,
,
设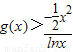 ,
,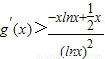 ,
,
令g′(x)=0,解得x=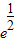 ,
,
当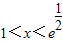 时,g′(x)>0,g(x)在(0,
时,g′(x)>0,g(x)在(0,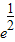 )上单调递增;
)上单调递增;
当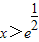 时,g′(x)<0,g(x)在(
时,g′(x)<0,g(x)在(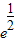 ,+∞)上单调递减;
,+∞)上单调递减;
∴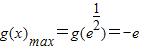
∴a-1>-e,即a>1-e.
故实数a的取值范围是(1-e,+∞).
点评:本题考查函数的增区间的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意导数性质的灵活运用.
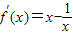 ,x>0,由f′(x)>0,能求出函数f(x)的单调递增区间.
,x>0,由f′(x)>0,能求出函数f(x)的单调递增区间.(2)依题意得f(x)-lnx>0,故
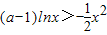 ,所以
,所以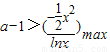 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.解答:解:(1)∵
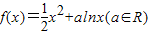 ,
,∴若a=-1时,
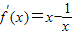 ,x>0,
,x>0,由f′(x)>0,得
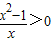 ,又x>0,解得x>1,
,又x>0,解得x>1,所以函数f(x)的单调递增区间为(1,+∞).
(2)依题意得f(x)-lnx>0,
即
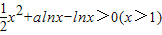 ,
,∴
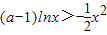
∵x>1,∴lnx>0
∴
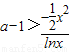 ,
,∴
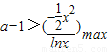 ,
,设
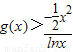 ,
,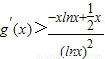 ,
,令g′(x)=0,解得x=
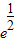 ,
,当
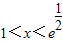 时,g′(x)>0,g(x)在(0,
时,g′(x)>0,g(x)在(0,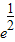 )上单调递增;
)上单调递增;当
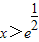 时,g′(x)<0,g(x)在(
时,g′(x)<0,g(x)在(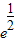 ,+∞)上单调递减;
,+∞)上单调递减;∴
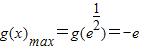
∴a-1>-e,即a>1-e.
故实数a的取值范围是(1-e,+∞).
点评:本题考查函数的增区间的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意导数性质的灵活运用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
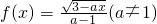 .
.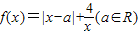 .
.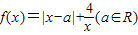 .
.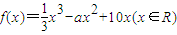 .
.