题目内容
已知A={（x，y）|x+y-2=0}，B={（x，y）|x-2y+4=0}，C={（x，y）|y=3x+b}，若（A∩B）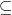
C，则b=________．
2
分析：根据集合的运算求A∩B，利用（A∩B）⊆C得点的坐标满足C，代入求值即可．
解答：因为A={（x，y）|x+y-2=0}，B={（x，y）|x-2y+4=0}，
所以A∩B={（x，y）|
}={（x，y）|
}={（0，2）}．
因为（A∩B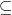）C，所以（0，2）∈C，将点的坐标代入得2=b，即b=2．
故答案为：2．
点评：本题主要考查集合的基本运算，注意点集的交集为直线的交点．
分析：根据集合的运算求A∩B，利用（A∩B）⊆C得点的坐标满足C，代入求值即可．
解答：因为A={（x，y）|x+y-2=0}，B={（x，y）|x-2y+4=0}，
所以A∩B={（x，y）|
}={（x，y）|}={（0，2）}．因为（A∩B）
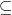C，所以（0，2）∈C，将点的坐标代入得2=b，即b=2．故答案为：2．
点评：本题主要考查集合的基本运算，注意点集的交集为直线的交点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目