题目内容
已知双曲线C的一条渐近线方程为x-2y=0,则该双曲线的离心率e= .
分析:由题设条件设双曲线方程为x2-4y2=k,转化为标准方程后,分焦点在x轴上和焦点在y轴上两种情况进行分类讨论,能够求出结果.
解答:解:∵双曲线C的一条渐近线方程为x-2y=0,
∴设双曲线方程为x2-4y2=k,
整理,得
-
=1,
当k>0时,a2=k,c2=k+
=
k,
e=
=
.
当k<0时,a2=-
,c2=-
-k=-
k,
e=
=
.
故答案为:
或
.
∴设双曲线方程为x2-4y2=k,
整理,得
| x2 |
| k |
| y2 | ||
|
当k>0时,a2=k,c2=k+
| k |
| 4 |
| 5 |
| 4 |
e=
| ||||
|
| ||
| 2 |
当k<0时,a2=-
| k |
| 4 |
| k |
| 4 |
| 5 |
| 4 |
e=
|
| 5 |
故答案为:
| ||
| 2 |
| 5 |
点评:本题考查双曲线的离心率的求法,解题时要认真审题,要熟练掌握双曲线的离心率、渐近线方程等基础知识,易错点是容易丢解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线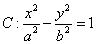
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
