题目内容
数列![]() 前
前![]() 项和为
项和为![]() ,首项为
,首项为![]() ,满足
,满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() ,使
,使![]() (其中
(其中![]() 是与自然数
是与自然数![]() 无关的常数),若存在,求出
无关的常数),若存在,求出![]() 与
与![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)求证:![]() 为有理数的充要条件是数列
为有理数的充要条件是数列![]() 中存在三项构成等比数列.
中存在三项构成等比数列.
同下
解析:
(1)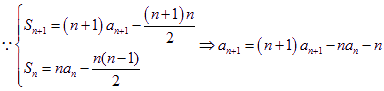
![]() ,数列
,数列![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为1
,公差为1
![]() --------------------------------------------------------------------------6分
--------------------------------------------------------------------------6分
(2)由![]() ,即
,即![]() ,
,
整理得:![]() ,当
,当![]() 时,该式恒成立;
时,该式恒成立;
即:当![]() 时,
时,![]() ,
,![]()
![]() 即为所求。--------------------------------10分
即为所求。--------------------------------10分
(3)证明:充分性:若三个不同的项![]() 成等比数列,且
成等比数列,且![]() ,则
,则
![]()
若![]() ,则
,则![]() ,
,![]() 与
与![]() 矛盾,
矛盾,
![]() ,且
,且![]() 都是非负整数,
都是非负整数,![]() 是有理数;----------------14分
是有理数;----------------14分
必要性:若![]() 是有理数,且
是有理数,且![]() ,则必存在正整数
,则必存在正整数![]() ,使
,使![]() ,令
,令![]()
则正项数列![]() ,是原数列
,是原数列![]() 的一个子数列,只要正项数列
的一个子数列,只要正项数列![]() 中存在三个不同的项构成等比数列则原数列中必有3个不同项构成等比数列。
中存在三个不同的项构成等比数列则原数列中必有3个不同项构成等比数列。
不失一般性,不妨设![]() ,记
,记![]()
又设![]() ,且
,且![]() 成等比数列,则
成等比数列,则![]()
为使![]() 为整数,可令
为整数,可令![]() ,于是
,于是![]()
可知![]() 成等比数列。证毕----------------------------------------------------18分
成等比数列。证毕----------------------------------------------------18分

练习册系列答案
相关题目
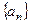 前
前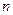 项和为
项和为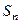 ,首项为
,首项为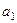 ,且
,且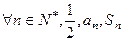 成等差数列.
成等差数列.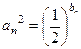 ,设
,设 ,求数列
,求数列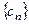 的前
的前 .
.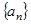 前
前 项和为
项和为 ,首项为
,首项为 ,且
,且 等差数列.
等差数列.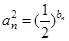 ,设
,设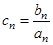 ,求数列
,求数列 的前
的前 .
.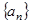 前
前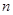 项和为
项和为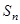 ,首项为
,首项为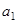 ,且
,且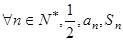 成等差数列.
成等差数列.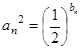 ,设
,设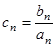 ,求数列
,求数列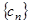 的前
的前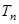 .
.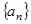 前
前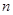 项和为
项和为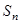 ,首项为
,首项为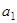 ,且
,且 成等差数列.
成等差数列.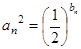 ,设
,设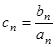 ,求数列
,求数列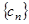 的前
的前 .
.