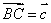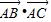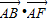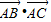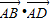题目内容
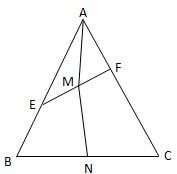 如图,在边长为1的正三角形ABC中,E,F分别是边AB,AC上的点,若
如图,在边长为1的正三角形ABC中,E,F分别是边AB,AC上的点,若| AE |
| AB |
| AF |
| AC |
(1)若A,M,N三点共线,求证m=n;
(2)若m+n=1,求|
| MN |
分析:(1)利用向量共线的充要条件得到
=λ
(λ∈R),据三角形的中线对应的向量等于相邻两边对应向量和的一半,将已知条件代入得到要证的结论.
(2)利用向量的运算法则:三角形法则将
用三角形的边对应的向量表示,利用向量模的平方等于向量的平方,将|
|2表示成m的二次函数,求出二次函数的最值.
| AM |
| AN |
(2)利用向量的运算法则:三角形法则将
| MN |
| MN |
解答:解:(1)由A,M,N三点共线,得
∥
,
设
=λ
(λ∈R),
即
(
+
)=
λ(
+
),
所以m
+n
=λ(
+
),
所以m=n.
(2)因为
=
-
=
(
+
)-
(
+
)=
(1-m)
+
(1-n)
,
又m+n=1,
所以
=
(1-m)
+
m
,
所以|
|2=
(1-m)2
2+
m2
2+
(1-m)m
•
=
(1-m)2+
m2+
(1-m)m=
(m-
)2+
故当m=
时,|
|min=
.
| AM |
| AN |
设
| AM |
| AN |
即
| 1 |
| 2 |
| AE |
| AF |
| 1 |
| 2 |
| AB |
| AC |
所以m
| AB |
| AC |
| AB |
| AC |
所以m=n.
(2)因为
| MN |
| AN |
| AM |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| AE |
| AF |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
又m+n=1,
所以
| MN |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
所以|
| MN |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| 1 |
| 2 |
| AB |
| AC |
=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 16 |
故当m=
| 1 |
| 2 |
| MN |
| ||
| 4 |
点评:本题考查向量共线的充要条件;三角形的中线对应向量等于相邻两边对应向量和的一半;考查向量的运算法则:三角形法则;向量模的平方等于向量的平方;二次函数最值的求法.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
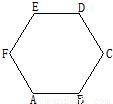
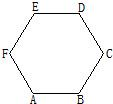
如图,在边长为1的正六边形ABCDEF中,下列向量的数量积中最大的是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|