Question

．(本小题满分12分)

有一种舞台灯，外形是正六棱柱，在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯，假若每只灯正常发光的概率为0.5，若一个侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用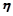表示更换的面数，用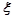表示更换费用。

(1)求①号面需要更换的概率；

(2)求6个面中恰好有2个面需要更换的概率；

(3)写出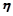的分布列，求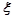的数学期望。

 

Answer 1

【答案】

(1)因为①号面不需要更换的概率为：

所以①号面需要更换的概率为：P=1-=

  (2)根据独立重复试验，6个面中恰好有2个面需要更换的概率为：

     P₆(2)=

  (3)因为，又P₆(0)=，P₆(1)= ，P₆(2)= ，P₆(3)= ，P₆(4)= ，P₆(5)= ，P₆ (6)=   

的分布列为：

	0	1	2	3	4	5	6
P（）

=100，E=100E=300

 

【解析】略