Question

15．已知函数f（x）=（$\frac{1}{2}$）^x，g（x）=${log_{\frac{1}{2}}}$x，记函数h（x）=$\left\{\begin{array}{l}g（x），f（x）≤g（x）\\ f（x），f（x）＞g（x）\end{array}$，则方程h（x）=2的解为x=$\frac{1}{4}$．

Answer 1

分析 确定f（x）与g（x）的图象交点的横坐标的范围，作出函数h（x）的图象，从而得到h（x）=2=g（x），解方程即可得到答案．

解答 解：记f（x）与g（x）的图象交点的横坐标为x=x₀，
∵f（$\frac{1}{2}$）=${（\frac{1}{2}）}^{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$＜1=${log}_{\frac{1}{2}}^{\frac{1}{2}}$，
∴x₀∈（$\frac{1}{2}$，1），
函数h（x）的图象如图所示：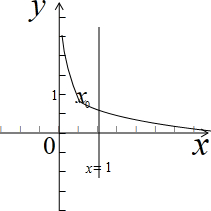

∴h（x）=2=${log}_{\frac{1}{2}}^{x}$，解得：x=$\frac{1}{4}$，
故答案为：x=$\frac{1}{4}$．

点评 本题考查新定义，考查不等式的解法，考查数形结合的数学思想，属于中档题．