题目内容
设函数f(x)=lnx,且x0,x1,x2∈(0,+∞),下列命题:
①若x1<x2,则
>
②存在x0∈(x1,x2),使得
=
③若x1>1,x2>1,则
<1
④对任意的x1,x2,都有f(
)>
其中正确的是
①若x1<x2,则
| 1 |
| x2 |
| f(x1)-f(x2) |
| x1-x2 |
②存在x0∈(x1,x2),使得
| 1 |
| x0 |
| f(x1)-f(x2) |
| x1-x2 |
③若x1>1,x2>1,则
| f(x1)-f(x2) |
| x1-x2 |
④对任意的x1,x2,都有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
其中正确的是
②③④
②③④
.(填写序号)分析:①利用割线的斜率判断.②利用割线的斜率判断.③利用割线的④利用函数的凸凹性判断.
解答: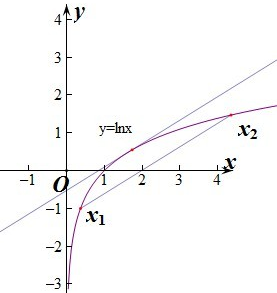 解:因为
解:因为
,表示x1与x2两点的斜率,
①不妨设x1=
,x2=1,
=
=2ln?2>1,若x=1,则
=1,此时
>
不成立.
所以①错误.
f′(x)=
,则f′(x0)=
,表示在x=x0处的切线斜率,由图象可知过x1与x2两点的割线和过x0点的切线可能平行,
所以②正确.
③因为函数的导数为f′(x)=
,当x>1时,f′(x)=
<1,即此时切线的斜率小于1,所以对应的割线的斜率也小于1,所以
<1成立,所以③正确.
④满足f(
)>
的函数为凸函数,所以④正确.
故答案为:②③④.
 解:因为
解:因为| f(x1)-f(x2) |
| x1-x2 |
①不妨设x1=
| 1 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
ln?
| ||
|
| 1 |
| x2 |
| 1 |
| x2 |
| f(x1)-f(x2) |
| x1-x2 |
所以①错误.
f′(x)=
| 1 |
| x |
| 1 |
| x0 |
所以②正确.
③因为函数的导数为f′(x)=
| 1 |
| x |
| 1 |
| x |
| f(x1)-f(x2) |
| x1-x2 |
④满足f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故答案为:②③④.
点评:本题主要考查了导数的几何意义以及函数的图象等有关知识,利用数形结合是解决本题的关键.

练习册系列答案
相关题目