题目内容
同时抛掷两枚大小形状都相同、质地均匀的骰子,求:
(1)一共有多少种不同的结果;
(2)点数之和4的概率;
(3)至少有一个点数为5的概率.
(1)36(2) (3)
(3)
解析试题分析:(1)每一个一个正方体骰子的结果有6种,因此同时抛掷两枚质地均匀的正方体骰子的结果有36种.
(2)用列举法求得在上面所有结果中其中点数之和是4的倍数的有9种,所以P(A)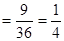 .
.
(3)由于所有36种结果是等可能的,其中至少有一个点数为5的结果有(1,5)(2,5)(3,5)
(4,5)(5,5)(6,5)(5,1)(5,2)(5,3)(5,4)(5,6)共11个,从而求得概率.古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法.
试题解析:(1)掷一枚骰子的结果有6种 1分 我们把两个骰子标上记1,2以便区分,由于1号
骰子的每一个结果都可以与2号骰子的任意一个结果配对,组成同时掷两枚骰子的一个结果 3分
因此同时掷两枚骰子的结果共有36种。 4分
(2)记事件A为“点数之和是4的倍数”,则A包含的基本事件为:(1,3)(2,2)(2,6)
(3,1)(3,5)(4,4)(5,3)(6,2)(6,6)共9个。 7分
所以P(A)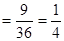 9分
9分
(3)记事件B为“至少有一个点数为5”,则事件B包含的基本事件为:(1,5)(2,5)(3,5)
(4,5)(5,5)(6,5)(5,1)(5,2)(5,3)(5,4)(5,6)共11个。 12分
所以P(B) 14分
14分
考点:古典概型及其概率计算公式

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案某牛奶厂要将一批牛奶用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且运费由厂商承担.若厂商恰能在约定日期(×月×日)将牛奶送到,则城市乙的销售商一次性支付给牛奶厂20万元;若在约定日期前送到,每提前一天销售商将多支付给牛奶厂1万元;若在约定日期后送到,每迟到一天销售商将少支付给牛奶厂1万元.为保证牛奶新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送牛奶,已知下表内的信息:
| 统计信息 汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
| 公路1 | 2 | 3 | 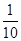 | 1.6 |
| 公路2 | 1 | 4 | 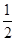 | 0.8 |
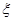 (单位:万元),求
(单位:万元),求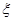 的分布列和数学期望
的分布列和数学期望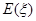 ;
;(II)如果你是牛奶厂的决策者,你选择哪条公路运送牛奶有可能让牛奶厂获得的毛收入更多?
(注:毛收入=销售商支付给牛奶厂的费用-运费)
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望 在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4人均选科目乙的概率;
(2)设
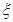 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求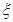 的分布列和数学期望.
的分布列和数学期望. 气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 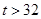 ℃ ℃ |
| 天数 | 6 | 12 |  |  |
 和
和 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.(Ⅰ) 若把频率看作概率,求
 ,
, 的值;
的值;(Ⅱ) 把日最高气温高于32℃称为本地区的 “高温天气”,根据已知条件完成下面
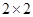 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.| | 高温天气 | 非高温天气 | 合计 |
| 旺销 | 1 | | |
| 不旺销 | | 6 | |
| 合计 | | | |

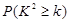 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某市 、
、 、
、 、
、 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |  |  |  |  |
| 人数 |  |  |  |  |
 名参加问卷调查.
名参加问卷调查.(1)问
 、
、 、
、 、
、 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?(2)从参加问卷调查的
 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;(3)在参加问卷调查的
 名学生中,从来自
名学生中,从来自 、
、 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列.
的分布列.  、乙答对的概率是
、乙答对的概率是 .(1)分别求甲、乙两人能通过一试进入二试的概率
.(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;(2)求甲、乙两人都能被录用的概率
;(2)求甲、乙两人都能被录用的概率 .
.
 为选取女生的人数,求X的分布列及数学期望.
为选取女生的人数,求X的分布列及数学期望.