题目内容
已知数列{an}是等差数列,首项a1=3,公差d=-1,设数列bn=2 ,Tn=b1b2…bn
,Tn=b1b2…bn(1)求证:数列{bn}是等比数列;
(2)Tn有无最大项,若有,求出最大值;若没有,说明理由.
【答案】分析:(1)利用等差数列的通项公式,确定数列{an}的通项公式,利用等比数列的定义,即可得出结论;
(2)确定Tn,Tn最大,则 最大,从而可得结论.
最大,从而可得结论.
解答:解:(1)由已知条件,数列{an}是等差数列,首项a1=3,公差d=-1
∴数列{an}的通项公式为:an=4-n,∴ ….(3分)
….(3分)
∴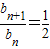 ,由定义知数列{bn}是等比数列…..(5分)
,由定义知数列{bn}是等比数列…..(5分)
(2)Tn=b1b2…bn= ,------------(7分)
,------------(7分)
若Tn最大,则 最大,当n=3或4时,f(3)=f(4)=6最大,------------(10分)
最大,当n=3或4时,f(3)=f(4)=6最大,------------(10分)
故Tn有最大项,最大值为T3=T4=64------------(12分)
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,考查学生分析解决问题的能力,属于中档题.
(2)确定Tn,Tn最大,则
 最大,从而可得结论.
最大,从而可得结论.解答:解:(1)由已知条件,数列{an}是等差数列,首项a1=3,公差d=-1
∴数列{an}的通项公式为:an=4-n,∴
 ….(3分)
….(3分)∴
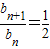 ,由定义知数列{bn}是等比数列…..(5分)
,由定义知数列{bn}是等比数列…..(5分)(2)Tn=b1b2…bn=
 ,------------(7分)
,------------(7分)若Tn最大,则
 最大,当n=3或4时,f(3)=f(4)=6最大,------------(10分)
最大,当n=3或4时,f(3)=f(4)=6最大,------------(10分)故Tn有最大项,最大值为T3=T4=64------------(12分)
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目