题目内容
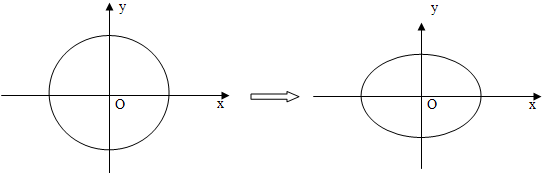
将圆x2+y2=4压扁得到椭圆C,方法是将该圆上的点的横坐标保持不变,纵坐标变为原来的
倍.
(1)求椭圆C的方程;
(2)设椭圆C的左焦点为F1,右焦点F2,直线l过点F1且垂直于椭圆的长轴,点P为直线l上的动点,过点P且垂直于l的动直线l1与线段PF2垂直平分线交于点M,求点M的轨迹C′的方程;
(3)是否存在过点(0,-2)的直线l2与椭圆C相交于A、B两点,使以AB为直径的圆过点O(O是坐标原点),若存在,求直线l2的方程;若不存在,说明理由.
| ||
| 2 |
(1)求椭圆C的方程;
(2)设椭圆C的左焦点为F1,右焦点F2,直线l过点F1且垂直于椭圆的长轴,点P为直线l上的动点,过点P且垂直于l的动直线l1与线段PF2垂直平分线交于点M,求点M的轨迹C′的方程;
(3)是否存在过点(0,-2)的直线l2与椭圆C相交于A、B两点,使以AB为直径的圆过点O(O是坐标原点),若存在,求直线l2的方程;若不存在,说明理由.

(1)设所求椭圆上的任意点的坐标为(x,y),圆上的对应点为(x′,y′),
依题意得
∴
,x/2+y/2=4,
∴x2+
=4,∴
+
=1
(2)依题意|MP|=|MF2|,F2(1,0),l:x=-1,M(x,y),
=|x+1|,
化简得点M的轨迹方程为y2=4x
(3)假设存在直线l2满足条件,显然直线l2的斜率存在,设其方程为y=kx-2,设A(x1,y1),B(x2,y2)
依题意得OA⊥OB,∴x1x2+y1y2=0,∵y1=kx1-2,y2=kx2-2,(1+k2)x1x2-2k(x1+x2)+4=0
由方程组得
得(3+4k2)x2-16kx+4=0,则x1+x2=
,x1x2=
∴
-2k×
+4=0,整理得k2=
,k=±
,
又△>0,∴k2>
,∴k=±
符合题意.
所以存在直线l2方程为y=±
x-2
依题意得
|
|
∴x2+
| 4y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
(2)依题意|MP|=|MF2|,F2(1,0),l:x=-1,M(x,y),
| (x-1)2+y2 |
化简得点M的轨迹方程为y2=4x
(3)假设存在直线l2满足条件,显然直线l2的斜率存在,设其方程为y=kx-2,设A(x1,y1),B(x2,y2)
依题意得OA⊥OB,∴x1x2+y1y2=0,∵y1=kx1-2,y2=kx2-2,(1+k2)x1x2-2k(x1+x2)+4=0
由方程组得
|
| 16k |
| 3+4k2 |
| 4 |
| 3+4k2 |
∴
| 4(1+k2) |
| 3+4k2 |
| 16k |
| 3+4k2 |
| 4 |
| 3 |
2
| ||
| 3 |
又△>0,∴k2>
| 1 |
| 4 |
2
| ||
| 3 |
所以存在直线l2方程为y=±
2
| ||
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
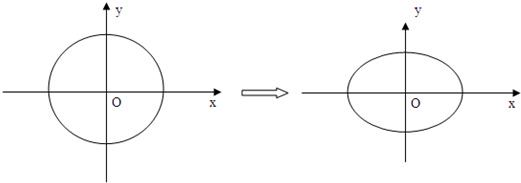

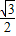 倍.
倍. (O是坐标原点),求直线l2的方程.
(O是坐标原点),求直线l2的方程.