题目内容
已知椭圆 与双曲线
与双曲线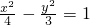 有相同的焦点,则a的值为
有相同的焦点,则a的值为
- A.

- B.

- C.4
- D.10
C
分析:求出双曲线的两焦点坐标,即为椭圆的焦点坐标,即可得到c的值,然后根据椭圆的定义得到a,最后利用a,b,c的关系即可求出a的值.
解答:双曲线方程化为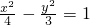 ,(1分)
,(1分)
由此得a=2,b= ,(3分)
,(3分)
c=7,
焦点为(-1,0),(1,0).(7分)
椭圆中,则a2=b2+c2=9+7=16.(11分)
则a的值为4.
故选C.
点评:此题考查学生掌握圆锥曲线的共同特征,会求椭圆的标准方程,是一道综合题.本题还考查双曲线的标准方程,以及双曲线的简单性质的应用,利用条件求出a,b,c值,是解题的关键.
分析:求出双曲线的两焦点坐标,即为椭圆的焦点坐标,即可得到c的值,然后根据椭圆的定义得到a,最后利用a,b,c的关系即可求出a的值.
解答:双曲线方程化为
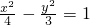 ,(1分)
,(1分)由此得a=2,b=
 ,(3分)
,(3分)c=7,
焦点为(-1,0),(1,0).(7分)
椭圆中,则a2=b2+c2=9+7=16.(11分)
则a的值为4.
故选C.
点评:此题考查学生掌握圆锥曲线的共同特征,会求椭圆的标准方程,是一道综合题.本题还考查双曲线的标准方程,以及双曲线的简单性质的应用,利用条件求出a,b,c值,是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 和
和 ,若
,若 是
是 的等比中项,
的等比中项, 是
是 与
与 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( ) B.
B. C.
C. D.
D.
 与双曲线
与双曲线 有相同的准线,则动点
有相同的准线,则动点 的
的