题目内容
已知函数f（x）=
ax2+2x，g（x）=lnx．
（1）求函数y=xg（x）﹣2x的单调增区间．
（2）如果函数y=f（x）在[1，+∞）上是单调增函数，求a的取值范围；
（3）是否存在实数a＞0，使得方程
=f′（x）﹣（2a+1）在区间（
，e）内有且只有两个不相等的实数根？若存在，请求出a的取值范围；若不存在，请说明理由．
ax2+2x，g（x）=lnx．（1）求函数y=xg（x）﹣2x的单调增区间．
（2）如果函数y=f（x）在[1，+∞）上是单调增函数，求a的取值范围；
（3）是否存在实数a＞0，使得方程
=f′（x）﹣（2a+1）在区间（，e）内有且只有两个不相等的实数根？若存在，请求出a的取值范围；若不存在，请说明理由．解：（1）∵y′=lnx﹣1 令y′＞0，则x＞e
∴函数y=xg（x）﹣2x的单调增区间为（e，+∞）
（2）当a=0时，f（x）=2x在[1，+∞）上是增函数，
当a＞0时，y=f（x）的对称轴方程为x=﹣
由于y=f（x）在[1，+∞）上是增函数，
∴﹣
≤1，解得a≤﹣2或a＞0，
∴a＞0
当a＜0时，不符合题意，
综上，a的取值范围为a≥0
（3）方程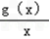
=f′（x）﹣（2a+1）
可化简为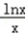
=ax+2﹣（2a+1）即为方程ax2+（1﹣2a）x﹣lnx=0．
设H（x）=ax2+（1﹣2a）x﹣lnx，（x＞0）
原方程在区间（
，e）内有且只有两个不相等的实数根，
即函数H（x）在区间（
，e）内有且只有两个零点．
H′（x）=2ax+（1﹣2a）﹣
=
=
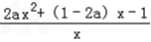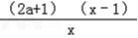
令H′（x）=0，因为a＞0，解得x=1或x=﹣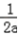
（舍）
当x∈（0，1）时，H′（x）＜0，H（x）是减函数；
当x∈（1，+∞）时，H′（x）＞0，，H（x）是增函数．，
H（x）在（
，e）内有且只有两个不相等的零点，
只需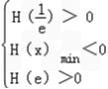
即1＜a＜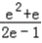 
∴函数y=xg（x）﹣2x的单调增区间为（e，+∞）
（2）当a=0时，f（x）=2x在[1，+∞）上是增函数，
当a＞0时，y=f（x）的对称轴方程为x=﹣
由于y=f（x）在[1，+∞）上是增函数，
∴﹣
≤1，解得a≤﹣2或a＞0，∴a＞0
当a＜0时，不符合题意，
综上，a的取值范围为a≥0
（3）方程
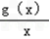=f′（x）﹣（2a+1）可化简为
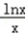=ax+2﹣（2a+1）即为方程ax2+（1﹣2a）x﹣lnx=0．设H（x）=ax2+（1﹣2a）x﹣lnx，（x＞0）
原方程在区间（
，e）内有且只有两个不相等的实数根，即函数H（x）在区间（
，e）内有且只有两个零点．H′（x）=2ax+（1﹣2a）﹣
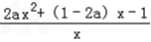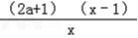
= = 令H′（x）=0，因为a＞0，解得x=1或x=﹣
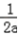（舍）当x∈（0，1）时，H′（x）＜0，H（x）是减函数；
当x∈（1，+∞）时，H′（x）＞0，，H（x）是增函数．，
H（x）在（
，e）内有且只有两个不相等的零点，只需
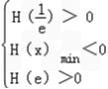即1＜a＜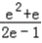 
练习册系列答案
相关题目