题目内容

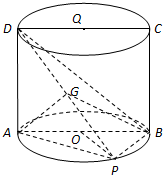精英家教网如图，四边形ABCD是圆柱OQ的轴截面，点P在圆柱OQ的底面圆周上，G是DP的中点，
圆柱OQ的底面圆的半径OA=2，侧面积为8
3
π，∠AOP=120°．
（1）求证：AG⊥BD；
（2）求二面角P-AG-B的平面角的余弦值．
分析：解法一：（1）由题设条件知可通过证明AG⊥面DBP证AG⊥BD；
（2）作辅助线，如图，找出∠PGB是二面角P-AG-B的平面角，由于其所在的三角形各边已知，且是一个直角三角形，故易求．
解法二：建立如图的空间坐标系，给出图中各点的坐标
（1）求出AG，BD两线段对应的向量的坐标，验证其内积为0即可得出两直线是垂直的；
（2）求出两个平面的法向量，然后求出两法向量夹角的余弦值的约对值即是二面角P-AG-B的平面角的余弦值．
解答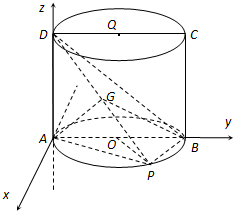：精英家教网解：（1）（解法一）：由题意可知8
3
π=2×2π×AD，
解得AD=2
3
，
在△AOP中，AP=
22+22-2×2×2×cos120°
，
∴AD=AP，
又∵G是DP的中点，
∴AG⊥DP．①
∵AB为圆O的直径，
∴AP⊥BP．
由已知知DA⊥面ABP，
∴DA⊥BP，
∴BP⊥面DAP．分
∴BP⊥AG．②
∴由①②可知：AG⊥面DBP，
∴AG⊥BD．
（2）由（1）知：AG⊥面DBP，
∴AG⊥BG，AG⊥PG，
∴∠PGB是二面角P-AG-B的平面角．
PG=
1
2
PD=
1
3
×
2
AP=
6
，
BP=OP=2，∠BPG=90°，．
∴BG=
PG2+BP2
=
10
．
cos∠PGB=
PG
BG
=
6
10
=
15
5
．
（解法二）：建立如图所示的直角坐标系，由题意可知8
3
π=2×2π×AD，
解得AD=2
3
，
则A（0，0，0），B（0，4，0），D（0，0，2
3
），P（
3
，3，0），
∵G是DP的中点，
∴可求得G（
3
2
，
3
2
，
3
）．
（1）
BP
=（
3
，-1，0），
BD
=（0，-4，2
3
），，
∴
AG
=（
3
2
，
3
2
，
3
）．
∵
AG
•
BP
=（
3
2
，
3
2
，
3
）•（0，-4，2
3
）=0，
∴AG⊥BD
（2）由（1）知，）
BP
=（
3
，-1，0），
AG
=（
3
2
，
3
2
，
3
）.
PG
=（-
3
2
，-
3
2
，
3
）
BG
=（
3
2
，-
5
2
，
3
）

∵
AG
•
PG
=0，
AG
•
BP
=0．
∴
BP
是平面APG的法向量．
设
n
=（x，y，1）是平面ABG的法向量，
由
n
•
AG
=0，
n
•
AB
=0，
解得
n
=（-2，0，1）分
cosθ=
BP
•
n
|
n
||
BP
|
=
-2
3
2
5
=-
15
5
．
所以二面角二面角P-AG-B的平面角的余弦值
15
5
点评：本题考查空间的线面关系、二面角、空间向量及坐标运算、余弦定理等知识，考查数形结合、化归转化的数学思想和方法，以及空间想象能力、推理论证能力和运算求解能力
练习册系列答案
相关题目
精英家教网如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
（1） 求证：A′C∥平面BDE；
（2） 求证：平面A′AC⊥平面BDE
（3） 求平面BDE与平面ABCD所成锐二面角的正切值．
精英家教网如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
12
PD．
（Ⅰ）证明PQ⊥平面DCQ；
（Ⅱ）求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值．
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
（1）求点C到面PDE的距离；  
（2）求二面角P-DE-A的余弦值．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
128°
128°
．
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=
12
PD．
（1）证明：平面PQC⊥平面DCQ；
（2）求二面角D-PQ-C的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网