题目内容
已知函数f(x)=ex-kx2,x∈R.
(1)若k=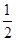 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1;
(2)若f(x)在区间(0,+∞)上单调递增,试求k的取值范围;
(3)求证: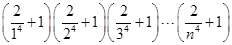 <e4(n∈N*)..
<e4(n∈N*)..
(1)若k=
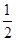 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1;(2)若f(x)在区间(0,+∞)上单调递增,试求k的取值范围;
(3)求证:
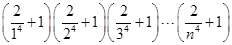 <e4(n∈N*)..
<e4(n∈N*)..(1)见解析(2)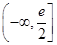 (3)见解析
(3)见解析
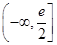 (3)见解析
(3)见解析(1)证明 f(x)=ex-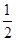 x2,则h(x)=f′(x)=ex-x,
x2,则h(x)=f′(x)=ex-x,
∴h′(x)=ex-1>0(x>0),∴h(x)=f′(x)在(0,+∞)上单调递增,∴f′(x)>f′(0)=1>0.∴f(x)=ex-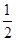 x2在(0,+∞)上单调递增,故f(x)>f(0)=1.
x2在(0,+∞)上单调递增,故f(x)>f(0)=1.
(2)解 f′(x)=ex-2kx,求使f′(x)>0(x>0)恒成立的k的取值范围.
若k≤0,显然f′(x)>0,f(x)在区间(0,+∞)上单调递增,当k>0时,记φ(x)=ex-2kx,则φ′(x)=ex-2k,当0<k<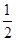 时,∵ex>e0=1,而2k<1,∴φ′(x)>0,则φ(x)在(0,+∞)上单调递增,于是f′(x)=φ(x)>φ(0)=1>0,∴f(x)在(0,+∞)单调递增;当k≥
时,∵ex>e0=1,而2k<1,∴φ′(x)>0,则φ(x)在(0,+∞)上单调递增,于是f′(x)=φ(x)>φ(0)=1>0,∴f(x)在(0,+∞)单调递增;当k≥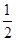 时,φ(x)=ex-2kx在(0,ln 2k)上单调递减,在(ln 2k,+∞)上单调递增,于是f′(x)=φ(x)=φ(ln 2k)=eln 2k-2kln 2k,由eln 2k-2kln 2k≥0得2k-2kln 2k≥0,则
时,φ(x)=ex-2kx在(0,ln 2k)上单调递减,在(ln 2k,+∞)上单调递增,于是f′(x)=φ(x)=φ(ln 2k)=eln 2k-2kln 2k,由eln 2k-2kln 2k≥0得2k-2kln 2k≥0,则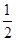 ≤k≤
≤k≤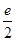 .综上,k的取值范围是
.综上,k的取值范围是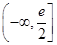 .
.
(3)证明 由(1)知,对于x∈(0,+∞),有f(x)=ex-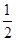 x2>1,∴e2x>2x2+1,则ln (2x2+1)<2x,
x2>1,∴e2x>2x2+1,则ln (2x2+1)<2x,
从而有ln <
<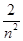 (n∈N*),
(n∈N*),
于是ln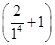 +ln
+ln 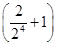 +ln
+ln 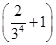 +…+ln
+…+ln  <
<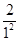 +
+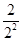 +…+
+…+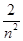 <
<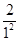 +
+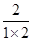 +
+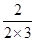 +…+
+…+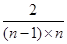 =2+
=2+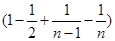 =4-
=4-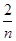 <4,故
<4,故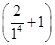 ·
·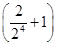 ·…·
·…· <e4(n∈N*)
<e4(n∈N*)
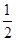 x2,则h(x)=f′(x)=ex-x,
x2,则h(x)=f′(x)=ex-x,∴h′(x)=ex-1>0(x>0),∴h(x)=f′(x)在(0,+∞)上单调递增,∴f′(x)>f′(0)=1>0.∴f(x)=ex-
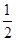 x2在(0,+∞)上单调递增,故f(x)>f(0)=1.
x2在(0,+∞)上单调递增,故f(x)>f(0)=1.(2)解 f′(x)=ex-2kx,求使f′(x)>0(x>0)恒成立的k的取值范围.
若k≤0,显然f′(x)>0,f(x)在区间(0,+∞)上单调递增,当k>0时,记φ(x)=ex-2kx,则φ′(x)=ex-2k,当0<k<
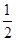 时,∵ex>e0=1,而2k<1,∴φ′(x)>0,则φ(x)在(0,+∞)上单调递增,于是f′(x)=φ(x)>φ(0)=1>0,∴f(x)在(0,+∞)单调递增;当k≥
时,∵ex>e0=1,而2k<1,∴φ′(x)>0,则φ(x)在(0,+∞)上单调递增,于是f′(x)=φ(x)>φ(0)=1>0,∴f(x)在(0,+∞)单调递增;当k≥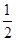 时,φ(x)=ex-2kx在(0,ln 2k)上单调递减,在(ln 2k,+∞)上单调递增,于是f′(x)=φ(x)=φ(ln 2k)=eln 2k-2kln 2k,由eln 2k-2kln 2k≥0得2k-2kln 2k≥0,则
时,φ(x)=ex-2kx在(0,ln 2k)上单调递减,在(ln 2k,+∞)上单调递增,于是f′(x)=φ(x)=φ(ln 2k)=eln 2k-2kln 2k,由eln 2k-2kln 2k≥0得2k-2kln 2k≥0,则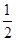 ≤k≤
≤k≤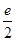 .综上,k的取值范围是
.综上,k的取值范围是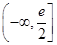 .
.(3)证明 由(1)知,对于x∈(0,+∞),有f(x)=ex-
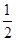 x2>1,∴e2x>2x2+1,则ln (2x2+1)<2x,
x2>1,∴e2x>2x2+1,则ln (2x2+1)<2x,从而有ln
 <
<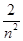 (n∈N*),
(n∈N*),于是ln
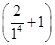 +ln
+ln 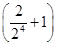 +ln
+ln 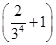 +…+ln
+…+ln  <
<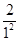 +
+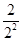 +…+
+…+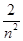 <
<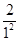 +
+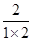 +
+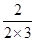 +…+
+…+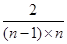 =2+
=2+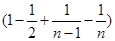 =4-
=4-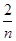 <4,故
<4,故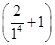 ·
·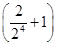 ·…·
·…· <e4(n∈N*)
<e4(n∈N*)
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
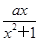 +a,g(x)=aln x-x(a≠0).
+a,g(x)=aln x-x(a≠0).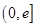 ,总有g(x1)<f(x2)成立.
,总有g(x1)<f(x2)成立.
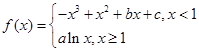 的图像过坐标原点
的图像过坐标原点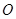 ,且在点
,且在点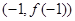 处的切线的斜率是
处的切线的斜率是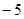 .
.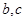 的值;
的值;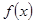 在区间
在区间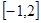 上的最大值;
上的最大值;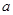 ,曲线
,曲线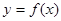 上是否存在两点
上是否存在两点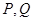 ,使得
,使得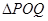 是以
是以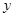 轴上?请说明理由.
轴上?请说明理由.
 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围; 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中 且
且 求
求 的取值范围.
的取值范围.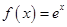 .
.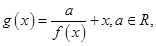 求
求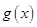 的极值.
的极值.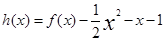 在
在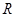 上为增函数。
上为增函数。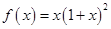 ,
,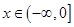 .
.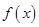 的极值点;
的极值点;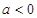 ,记
,记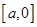 上的最小值为
上的最小值为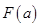 ,求
,求 的最小值.
的最小值. ,求
,求 ( )
( )