题目内容
已知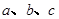 是直线,
是直线,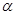 是平面,
是平面,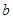 、
、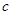
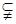
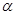 ,则“
,则“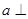 平面
平面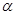 ”是“
”是“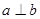 且
且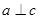 ”
”
的……………………………………………………………………………………………( )
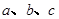 是直线,
是直线,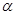 是平面,
是平面,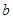 、
、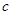
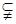
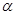 ,则“
,则“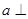 平面
平面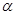 ”是“
”是“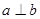 且
且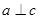 ”
”的……………………………………………………………………………………………( )
| A.充要条件. | B.充分非必要条件. | C.必要非充分条件. | D.非充分非必要条件. |
B
此题考查充分条件和必要条件的判断,考查线面垂直的判定和性质。充分条件和必要条件的判定方法
(1)定义法(通用的方法):
①若 ,则
,则 是
是 的充分不必要条件;
的充分不必要条件;
②若 ,则
,则 是
是 的必要不充分条件;
的必要不充分条件;
③若 ,则
,则 是
是 的充分必要条件;
的充分必要条件;
④若 ,则
,则 是
是 的既不充分又不必要条件;
的既不充分又不必要条件;
(2)集合判断法:若已知条件给的是两个集合问题,可以利用此方法判断:
设条件 和
和 对应的集合分别是
对应的集合分别是
①若 ,则
,则 是
是 充分条件;若
充分条件;若 ,则
,则 是
是 的充分不必要条件;
的充分不必要条件;
②若 ,则
,则 是
是 必要条件;若
必要条件;若 ,则
,则 是
是 的必要不充分条件;
的必要不充分条件;
③若 ,则
,则 是
是 的充分必要条件;
的充分必要条件;
④若 ,则
,则 是
是 的既不充分又不必要条件;
的既不充分又不必要条件;
(3)命题真假法:利用原命题和真命题的真假来判断:设若 则
则 为原命题,
为原命题,
①若原命题真,逆命题假,则 是
是 的充分不必要条件;
的充分不必要条件;
②若原命题假,逆命题真,则 是
是 的必要不充分条件;
的必要不充分条件;
③若原命题真,逆命题真,则 是
是 的充分必要条件;
的充分必要条件;
④若原命题假,逆命题假,则 是
是 的既不充分又不必要条件;
的既不充分又不必要条件;
此题中由:如果一直线垂直于某平面则该直线垂直这个平面内的所有直线,所以由“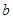 、
、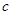
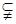
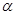 ,
,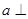 平面
平面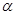 ”可以推出“
”可以推出“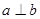 且
且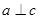 ”,所以是充分条件;根据线面垂直的判定定理可知,如果一条直线和某平面内的两条相交直线垂直,那么该直线和此平面垂直,所以由已知可知道
”,所以是充分条件;根据线面垂直的判定定理可知,如果一条直线和某平面内的两条相交直线垂直,那么该直线和此平面垂直,所以由已知可知道 不一定相交,所以不是必要条件,所以选B;
不一定相交,所以不是必要条件,所以选B;
(1)定义法(通用的方法):
①若
 ,则
,则 是
是 的充分不必要条件;
的充分不必要条件;②若
 ,则
,则 是
是 的必要不充分条件;
的必要不充分条件;③若
 ,则
,则 是
是 的充分必要条件;
的充分必要条件;④若
 ,则
,则 是
是 的既不充分又不必要条件;
的既不充分又不必要条件;(2)集合判断法:若已知条件给的是两个集合问题,可以利用此方法判断:
设条件
 和
和 对应的集合分别是
对应的集合分别是
①若
 ,则
,则 是
是 充分条件;若
充分条件;若 ,则
,则 是
是 的充分不必要条件;
的充分不必要条件;②若
 ,则
,则 是
是 必要条件;若
必要条件;若 ,则
,则 是
是 的必要不充分条件;
的必要不充分条件;③若
 ,则
,则 是
是 的充分必要条件;
的充分必要条件;④若
 ,则
,则 是
是 的既不充分又不必要条件;
的既不充分又不必要条件;(3)命题真假法:利用原命题和真命题的真假来判断:设若
 则
则 为原命题,
为原命题,①若原命题真,逆命题假,则
 是
是 的充分不必要条件;
的充分不必要条件;②若原命题假,逆命题真,则
 是
是 的必要不充分条件;
的必要不充分条件;③若原命题真,逆命题真,则
 是
是 的充分必要条件;
的充分必要条件;④若原命题假,逆命题假,则
 是
是 的既不充分又不必要条件;
的既不充分又不必要条件;此题中由:如果一直线垂直于某平面则该直线垂直这个平面内的所有直线,所以由“
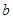 、
、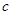
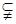
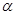 ,
,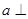 平面
平面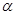 ”可以推出“
”可以推出“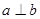 且
且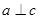 ”,所以是充分条件;根据线面垂直的判定定理可知,如果一条直线和某平面内的两条相交直线垂直,那么该直线和此平面垂直,所以由已知可知道
”,所以是充分条件;根据线面垂直的判定定理可知,如果一条直线和某平面内的两条相交直线垂直,那么该直线和此平面垂直,所以由已知可知道 不一定相交,所以不是必要条件,所以选B;
不一定相交,所以不是必要条件,所以选B;
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
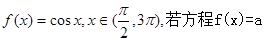 有三个不同的根,则“三个根从小到大依次成等比数列”是“
有三个不同的根,则“三个根从小到大依次成等比数列”是“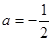 ”的 ( )
”的 ( ) B是
B是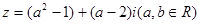 ,则“
,则“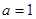 ”是“
”是“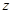 为纯虚数”的
为纯虚数”的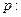
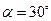 是
是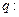
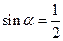 成立的 ( )
成立的 ( ) 的取值范围是
的取值范围是 



 说法正确的是_____
说法正确的是_____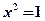 则
则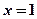 ”否命题为:
”否命题为: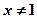 ;
;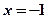 ”是
”是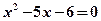 的必要不充分条件;
的必要不充分条件;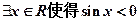 ”的否定是:
”的否定是: ,均有“
,均有“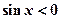 ”;
”;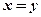 ,则
,则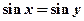 ”的逆否命题为真。
”的逆否命题为真。 ”是“
”是“ ”的必要不充分条件;
”的必要不充分条件; ”是“直线
”是“直线 与直线
与直线 互相垂直”的充要条件;
互相垂直”的充要条件; ”的否定
”的否定 :“
:“ ”.
”.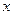 的一元二次不等式
的一元二次不等式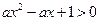 对于一切实数
对于一切实数