题目内容
 如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2| 2 |
(Ⅰ)求证:平面B1EF⊥平面BDD1B1;
(Ⅱ)求点D1到平面B1EF的距离d;
(Ⅲ)求三棱锥B1-EFD1的体积V.
分析:(1)方法一:欲证明平面B1EF⊥平面BDD1B1,先证直线与平面垂直,观察平面BDD1B1为正四棱柱ABCD-A1B1C1D1的对角面,所以AC⊥平面BDD1B1,故连接AC,由EF∥AC,可得EF⊥平面BDD1B1
方法二:欲证明平面B1EF⊥平面BDD1B1,先证直线与平面垂直,由题意易得EF⊥BD,又EF⊥D1D,所以EF⊥平面BDD1B1
(2)本题的设问是递进式的,第(1)问是为第(2)问作铺垫的.由第(1)问可知,点D1到平面B1EF的距离d即为点D1到平面B1EF与平面BDD1B1的交线B1G的距离,故作D1H⊥B1G,垂足为H,所以点D1到平面B1EF的距离d=D1H.下面求D1H的长度.
解法一:在矩形BDD1B1及Rt△D1HB1中,利用三角函数可解.
解法二:在矩形BDD1B1及Rt△D1HB1中,利用三角形相似可解.
解法三:在矩形BDD1B1及△D1GB1中,观察面积大小关系可解.
(3)本题的设问是递进式的,第(2)问是为第(3)问作铺垫的.解决三棱锥求体积的问题,关键在于找到合适的高与对应的底面,由第(2)问可知,D1H即为三棱锥B1-EFD1的高,所以B1EF为对应的底面.
方法二:欲证明平面B1EF⊥平面BDD1B1,先证直线与平面垂直,由题意易得EF⊥BD,又EF⊥D1D,所以EF⊥平面BDD1B1
(2)本题的设问是递进式的,第(1)问是为第(2)问作铺垫的.由第(1)问可知,点D1到平面B1EF的距离d即为点D1到平面B1EF与平面BDD1B1的交线B1G的距离,故作D1H⊥B1G,垂足为H,所以点D1到平面B1EF的距离d=D1H.下面求D1H的长度.
解法一:在矩形BDD1B1及Rt△D1HB1中,利用三角函数可解.
解法二:在矩形BDD1B1及Rt△D1HB1中,利用三角形相似可解.
解法三:在矩形BDD1B1及△D1GB1中,观察面积大小关系可解.
(3)本题的设问是递进式的,第(2)问是为第(3)问作铺垫的.解决三棱锥求体积的问题,关键在于找到合适的高与对应的底面,由第(2)问可知,D1H即为三棱锥B1-EFD1的高,所以B1EF为对应的底面.
解答: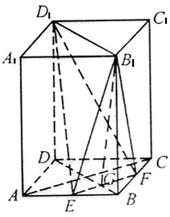 解:(Ⅰ)证法一:
解:(Ⅰ)证法一:
连接AC.
∵正四棱柱ABCD-A1B1C1D1的底面是正方形,
∴AC⊥BD,又AC⊥D1D,故AC⊥平面BDD1B1.
∵E,F分别为AB,BC的中点,故EF∥AC,
∴EF⊥平面BDD1B1,
∴平面B1EF⊥平面BDD1B1.
证法二:
∵BE=BF,∠EBD=∠FBD=45°,
∴EF⊥BD.又EF⊥D1D
∴EF⊥平面BDD1B1,
∴平面B1EF⊥平面BDD1B1.
(Ⅱ)在对角面BDD1B1中,
作D1H⊥B1G,垂足为H.
∵平面B1EF⊥平面BDD1B1,
且平面B1EF∩平面BDD1B1=B1G,
∴D1H⊥平面B1EF,且垂足为H,
∴点D1到平面B1EF的距离d=D1H.
解法一:
在Rt△D1HB1中,D1H=D1B1•sin∠D1B1H.
∵D1B1=
A1B1=
•2
=4,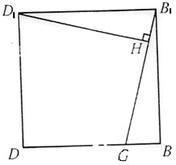
sin∠D1B1H=sin∠B1GB=
=
=
,
∴d=D1H=4•
=
.
解法二:
∵△D1HB1~△B1BG,
∴
=
,
∴d=D1H=
=
=
.
解法三:
连接D1G,则三角形D1GB1的面积等于正方形DBB1D1面积的一半,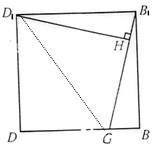
即
•B1G•D1H=
B1B2,
∴d=D1H=
=
.
(Ⅲ)V=VB1-EFD1=VD1-B1EF=
•d•S△B1EF
=
•
•
•2•
=
.
 解:(Ⅰ)证法一:
解:(Ⅰ)证法一:连接AC.
∵正四棱柱ABCD-A1B1C1D1的底面是正方形,
∴AC⊥BD,又AC⊥D1D,故AC⊥平面BDD1B1.
∵E,F分别为AB,BC的中点,故EF∥AC,
∴EF⊥平面BDD1B1,
∴平面B1EF⊥平面BDD1B1.
证法二:
∵BE=BF,∠EBD=∠FBD=45°,
∴EF⊥BD.又EF⊥D1D
∴EF⊥平面BDD1B1,
∴平面B1EF⊥平面BDD1B1.
(Ⅱ)在对角面BDD1B1中,
作D1H⊥B1G,垂足为H.
∵平面B1EF⊥平面BDD1B1,
且平面B1EF∩平面BDD1B1=B1G,
∴D1H⊥平面B1EF,且垂足为H,
∴点D1到平面B1EF的距离d=D1H.
解法一:
在Rt△D1HB1中,D1H=D1B1•sin∠D1B1H.
∵D1B1=
| 2 |
| 2 |
| 2 |

sin∠D1B1H=sin∠B1GB=
| B1B |
| GB1 |
| 4 | ||
|
| 4 | ||
|
∴d=D1H=4•
| 4 | ||
|
16
| ||
| 17 |
解法二:
∵△D1HB1~△B1BG,
∴
| D1H |
| B1B |
| D1B1 |
| B1G |
∴d=D1H=
| B1B2 |
| B1G |
| 42 | ||
|
16
| ||
| 17 |
解法三:
连接D1G,则三角形D1GB1的面积等于正方形DBB1D1面积的一半,

即
| 1 |
| 2 |
| 1 |
| 2 |
∴d=D1H=
| B1B2 |
| B1G |
16
| ||
| 17 |
(Ⅲ)V=VB1-EFD1=VD1-B1EF=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 16 | ||
|
| 1 |
| 2 |
| 17 |
| 16 |
| 3 |
点评:本小题主要考查正四棱柱的基本知识,考查空间想象能力、逻辑思维能力和运算能力.

练习册系列答案
相关题目
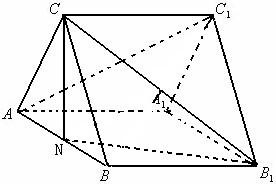 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
