题目内容
(本小题共13分)已知椭圆 的左焦点为
的左焦点为 ,过点M(-3,0)作一条斜率大于0的直线
,过点M(-3,0)作一条斜率大于0的直线 与W交于不同的两点A、B,延长BF交W于点C.
与W交于不同的两点A、B,延长BF交W于点C.
(1)求椭圆W的离心率;
(2)求证:点A与点C关于 轴对称.
轴对称.
(1) ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)由椭圆方程中 的关系可得
的关系可得 ,解得
,解得 ,可求离心率;(2)设直线
,可求离心率;(2)设直线 的方程为
的方程为 ,与椭圆方程联立,得到
,与椭圆方程联立,得到 (
( ),
),
 坐标间关系,设出点
坐标间关系,设出点 关于
关于 轴的对称点
轴的对称点 ,可判断
,可判断 三点共线,即点
三点共线,即点 与
与 重合,可证得结论成立.
重合,可证得结论成立.
试题解析:(1)由题意 ,
,
解得 .
.
所以椭圆 .
.
离心率 .(5分)
.(5分)

(2)设直线 的方程为
的方程为 .
.
联立
得 .
.
由直线 与椭圆W交于A、B两点,可知
与椭圆W交于A、B两点,可知
△ ,解得
,解得 .
.
设点A,B的坐标分别为( ),
), ,
,
则 ,
, ,
,
 .
.
因为F(-2,0),设点A关于 轴的对称点为C′,则C′(
轴的对称点为C′,则C′( ),
),
所以 ,
, .
.
又因为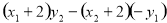



 ,
,
所以B,F,C′共线,从而C与C′重合,故点A与点C关于 轴对称.(13分)
轴对称.(13分)
考点:椭圆的几何性质、直线与椭圆位置关系.

练习册系列答案
相关题目
 在
在 上的最大值和最小值是( )
上的最大值和最小值是( ) 、
、 B.
B. 、
、
 D.
D. 、
、
 满足约束条件
满足约束条件 ,则
,则 的最大值是( )
的最大值是( ) ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
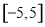 内随机取出一个实数
内随机取出一个实数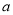 ,则
,则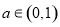 的概率为( )
的概率为( ) 具有性质P:对任意
具有性质P:对任意 ,其中
,其中 ,均有
,均有 属于A,若
属于A,若 ,则
,则 __________.
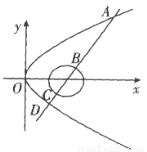
__________.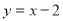 与圆
与圆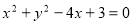 及抛物线
及抛物线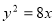 依次交于A、B、C、D四点,则
依次交于A、B、C、D四点,则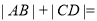 ( )
( )
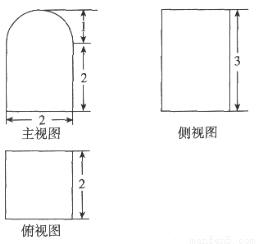
 ),可得这个几何体的体积是__________
),可得这个几何体的体积是__________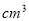 .
.
 :命题
:命题 .则下列判断正确的是
.则下列判断正确的是 是真命题
是真命题  是真命题
是真命题