题目内容
若a,b,c是三角形ABC的角A、B、C所对的三边,向量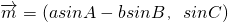 ,
,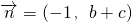 ,若
,若 ⊥
⊥ ,则三角形ABC为三角形
,则三角形ABC为三角形
- A.锐角
- B.直角
- C.钝角
- D.不能确定
C
分析:因为 ⊥
⊥ ,则两个向量的数量积为0,化简后,利用正弦定理和余弦定理三角形的一个角为钝角,可判断三角形的形状.
,则两个向量的数量积为0,化简后,利用正弦定理和余弦定理三角形的一个角为钝角,可判断三角形的形状.
解答:由 ⊥
⊥ ,得
,得 •
• =0,代入得到:-asinA+bsinB+bsinC+csinC=0,
=0,代入得到:-asinA+bsinB+bsinC+csinC=0,
根据正弦定理化简得:c2+b2=a2-bc;再根据余弦定理得:cosA= =-
=- ,且A∈(0,π)
,且A∈(0,π)
所以A为钝角,三角形为钝角三角形.
故选C
点评:考查学生掌握平面向量数量积的运算,以及灵活运用正弦定理、余弦定理解决数学问题.会判断三角形的形状.
分析:因为
 ⊥
⊥ ,则两个向量的数量积为0,化简后,利用正弦定理和余弦定理三角形的一个角为钝角,可判断三角形的形状.
,则两个向量的数量积为0,化简后,利用正弦定理和余弦定理三角形的一个角为钝角,可判断三角形的形状.解答:由
 ⊥
⊥ ,得
,得 •
• =0,代入得到:-asinA+bsinB+bsinC+csinC=0,
=0,代入得到:-asinA+bsinB+bsinC+csinC=0,根据正弦定理化简得:c2+b2=a2-bc;再根据余弦定理得:cosA=
 =-
=- ,且A∈(0,π)
,且A∈(0,π)所以A为钝角,三角形为钝角三角形.
故选C
点评:考查学生掌握平面向量数量积的运算,以及灵活运用正弦定理、余弦定理解决数学问题.会判断三角形的形状.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
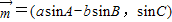 ,
,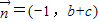 ,若
,若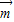 ⊥
⊥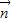 ,则三角形ABC为( )三角形
,则三角形ABC为( )三角形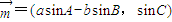 ,
,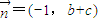 ,若
,若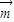 ⊥
⊥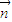 ,则三角形ABC为( )三角形
,则三角形ABC为( )三角形