题目内容
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为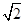 ,且过点(4,-
,且过点(4,-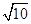 ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证: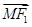 ·
· =0;
=0;
(3)求△F1MF2的面积.
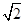 ,且过点(4,-
,且过点(4,-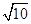 ).
).(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:
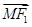 ·
· =0;
=0;(3)求△F1MF2的面积.
(1)x2-y2=6 (2)见解析 (3)6
(1)∵e=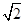 ,
,
∴设双曲线方程为x2-y2=λ.
又∵双曲线过(4,-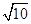 )点,
)点,
∴λ=16-10=6,
∴双曲线方程为x2-y2=6.
(2)证明:∵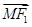 =(-3-2
=(-3-2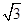 ,-m),
,-m),
 =(2
=(2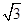 -3,-m),
-3,-m),
∴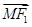 ·
· =(3+2
=(3+2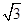 )(3-2
)(3-2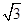 )+m2=-3+m2.
)+m2=-3+m2.
∵M在双曲线上,∴9-m2=6,
∴m2=3,∴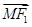 ·
· =0.
=0.
(3)∵在△F1MF2中,|F1F2|=4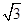 ,且|m|=
,且|m|=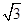 ,
,
∴S△F1MF2=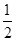 ·|F1F2|·|m|
·|F1F2|·|m|
=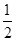 ×4
×4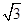 ×
×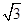 =6.
=6.
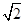 ,
,∴设双曲线方程为x2-y2=λ.
又∵双曲线过(4,-
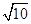 )点,
)点,∴λ=16-10=6,
∴双曲线方程为x2-y2=6.
(2)证明:∵
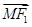 =(-3-2
=(-3-2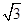 ,-m),
,-m), =(2
=(2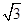 -3,-m),
-3,-m),∴
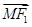 ·
· =(3+2
=(3+2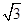 )(3-2
)(3-2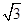 )+m2=-3+m2.
)+m2=-3+m2.∵M在双曲线上,∴9-m2=6,
∴m2=3,∴
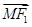 ·
· =0.
=0.(3)∵在△F1MF2中,|F1F2|=4
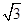 ,且|m|=
,且|m|=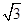 ,
,∴S△F1MF2=
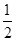 ·|F1F2|·|m|
·|F1F2|·|m|=
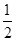 ×4
×4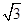 ×
×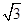 =6.
=6.
练习册系列答案
相关题目
 的左焦点
的左焦点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,双曲线左顶点为
,双曲线左顶点为 ,若
,若 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )

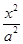 -y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
-y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )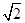 B.
B.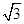 C.2 D.
C.2 D.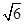
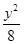 =1(x>1)
=1(x>1)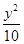 =1(x>1)
=1(x>1)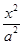 -
- =1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )
=1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )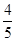
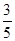
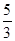
 的渐近线与方程为
的渐近线与方程为 的圆相切,则此双曲线的离心率为 .
的圆相切,则此双曲线的离心率为 .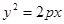 的焦点与双曲线
的焦点与双曲线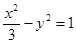 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )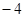
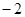
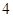
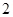
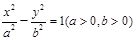 与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且
与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且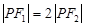 ,则双曲线的离心率为______.
,则双曲线的离心率为______.