题目内容
等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求和: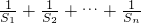 .
.
解:(1)设{an}的公差为d,{bn}的公比为q,则d为正整数,an=3+(n-1)d,bn=qn-1
依题意有 ①
①
解得 ,或
,或 (舍去)
(舍去)
故an=3+2(n-1)=2n+1,bn=8n-1
(2)Sn=3+5+…+(2n+1)=n(n+2)
∴ =
= =
= =
=
分析:(1)设{an}的公差为d,{bn}的公比为q,由题设条件建立方程组 ,解这个方程组得到d和q的值,从而求出an与bn.
,解这个方程组得到d和q的值,从而求出an与bn.
(2)由Sn=n(n+2),知 ,由此可求出
,由此可求出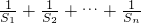 的值.
的值.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.
依题意有
 ①
①解得
 ,或
,或 (舍去)
(舍去)故an=3+2(n-1)=2n+1,bn=8n-1
(2)Sn=3+5+…+(2n+1)=n(n+2)
∴
 =
= =
= =
=
分析:(1)设{an}的公差为d,{bn}的公比为q,由题设条件建立方程组
 ,解这个方程组得到d和q的值,从而求出an与bn.
,解这个方程组得到d和q的值,从而求出an与bn.(2)由Sn=n(n+2),知
 ,由此可求出
,由此可求出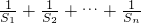 的值.
的值.点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目