题目内容
(本大题9分)已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ,
,
(1)求 的表达式;
的表达式;
(2)设0<a<b,当 时,
时, 的值域为
的值域为 ,求a,b的值.
,求a,b的值.
【答案】
(1)f(x)=
(2)a=1,b=
【解析】(1)因为f(x)为奇函数,所以用-x代替x,用-f(x)代替f(x)代入 ,即可得到x<0的解析式,从而得到f(x)在R上的解析式.
,即可得到x<0的解析式,从而得到f(x)在R上的解析式.
(2)由于0<a<b,当 时,所以
时,所以 ,由于开口向下,所以先根据f(a)=
,由于开口向下,所以先根据f(a)= 确定a可能的取值,然后再进一步研究比较简单.否则要按照轴定区间动的讨论方法分三种情况进行讨论.
确定a可能的取值,然后再进一步研究比较简单.否则要按照轴定区间动的讨论方法分三种情况进行讨论.

练习册系列答案
相关题目
(本小题9分)某家公司每月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量。
|
羊毛颜色 |
每匹需要 / kg |
供应量/ kg |
|
|
布料A |
布料B |
||
|
红 |
4 |
4 |
1400 |
|
绿 |
6 |
3 |
1800 |
|
黄 |
2 |
6 |
1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最大的利润是多少?
.(本小题9分)某家公司每月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量
|
羊毛颜色 |
每匹需要 / kg |
供应量/ kg |
|
|
布料A |
布料B |
||
|
红 |
4 |
4 |
1400 |
|
绿 |
6 |
3 |
1800 |
|
黄 |
2 |
6 |
1800 |
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最大的利润是多少?
 ),(9,
),(9, )为直径的圆.过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
)为直径的圆.过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.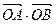 的最大值与最小值.
的最大值与最小值.