题目内容
 (2011•潍坊二模)如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=2,NB=1,MB与ND交于P点.
(2011•潍坊二模)如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=2,NB=1,MB与ND交于P点.(I)在棱AB上找一点Q,使QP∥平面AMD,并给出证明;
(Ⅱ)求平面BNC与平面MNC所成锐二面角的余弦值.
分析:(I)设Q为AB上的一点,满足BQ=
AB.由线面平行的性质证出MD∥NB,结合题中数据利用平行线的性质,得到
=
,从而在△MAB中得到QP∥AM.最后利用线面平行判定定理,证出QP∥平面AMD,说明在棱AB上存在满足条件的点;
(II)建立如图所示空间直角坐标系,算出向量
、
和
的坐标.利用垂直向量数量积为0的方法建立方程组,算出
=(1,-2,-2)为平面CMN的一个法向量.根据线面垂直的判定定理证出DC⊥平面BNC,从而得到
=(0,2,0)是平面BNC的一个法向量,最后用空间向量的夹角公式加以计算,即可算出平面BNC与平面MNC所成锐二面角的余弦值.
| 1 |
| 3 |
| QB |
| QA |
| BP |
| PM |
(II)建立如图所示空间直角坐标系,算出向量
| CM |
| CN |
| DC |
| m |
| DC |
解答:解:(I)当AB上的点满足BQ=
AB时,满足QP∥平面AMD,
∵MD⊥平面ABCD,NB⊥平面ABCD,∴MD∥NB.
∴
=
=
,且
=
=
,
∴
=
=
,在△MAB中,可得QP∥AM.
又∵QP?平面AMD,AM?平面AMD.
∴QP∥平面AMD,即存在棱AB上找一点Q,当BQ=
AB时,有QP∥平面AMD;
(II)以DA、DC、DM所在直线分别为x、y、z轴,建立如图所示空间直角坐标系
可得D(0,0,0),B(2,2,0),C(0,2,0),M(0,0,2),N(2,2,1)
∴
=(0,-2,2),
=(2,0,1),
=(0,2,0)
设平面CMN的一个法向量为
=(x,y,z)
∴
,取z=-2,得x=1,y=-2
由此可得
=(1,-2,-2)为平面CMN的一个法向量
∵NB⊥平面ABCD,CD?平面ABCD,∴NB⊥CD
又∵BC⊥CD,BC∩NB=B
∴DC⊥平面BNC,可得
=(0,2,0)是平面BNC的一个法向量
∵cos<
,
>=
=
=
∴平面BNC与平面MNC所成锐二面角的余弦值等于
.
| 1 |
| 3 |

∵MD⊥平面ABCD,NB⊥平面ABCD,∴MD∥NB.
∴
| BP |
| PM |
| NB |
| MD |
| 1 |
| 2 |
| QB |
| QA |
| ||
2-
|
| 1 |
| 2 |
∴
| QB |
| QA |
| BP |
| PM |
| 1 |
| 2 |
又∵QP?平面AMD,AM?平面AMD.
∴QP∥平面AMD,即存在棱AB上找一点Q,当BQ=
| 1 |
| 3 |
(II)以DA、DC、DM所在直线分别为x、y、z轴,建立如图所示空间直角坐标系
可得D(0,0,0),B(2,2,0),C(0,2,0),M(0,0,2),N(2,2,1)
∴
| CM |
| CN |
| DC |

设平面CMN的一个法向量为
| m |
∴
|
由此可得
| m |
∵NB⊥平面ABCD,CD?平面ABCD,∴NB⊥CD
又∵BC⊥CD,BC∩NB=B
∴DC⊥平面BNC,可得
| DC |
∵cos<
| m |
| DC |
| ||||
|
| 4 |
| 3×2 |
| 2 |
| 3 |
∴平面BNC与平面MNC所成锐二面角的余弦值等于
| 2 |
| 3 |
点评:本题在特殊多面体中,探索线面平行并求二面角的余弦值,着重考查了线面平行、垂直的判定与性质和利用空间向量研究平面与平面所成角等知识,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
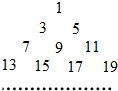 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足