Question

（07年福建卷理）（本题满分12分）

 等差数列的前项和为．

（Ⅰ）求数列的通项与前项和；

（Ⅱ）设，求证：数列中任意不同的三项都不可能成为等比数列．

Answer 1

本小题考查数列的基本知识，考查等差数列的概念、通项公式与前项和公式，考查等比数列的概念与性质，考查化归的数学思想方法以及推理和运算能力．

解析：（Ⅰ）由已知得，，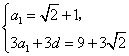

       故．

       （Ⅱ）由（Ⅰ）得．

       假设数列中存在三项（互不相等）成等比数列，则．

       即．

      

       ，

             ．

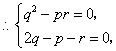
       与矛盾．

       所以数列中任意不同的三项都不可能成等比数列．