题目内容
设函数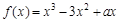
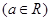 .
.
(1)当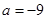 时,求函数
时,求函数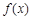 的极大值;
的极大值;
(2)若函数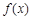 的图象与函数
的图象与函数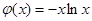 的图象有三个不同的交点,求
的图象有三个不同的交点,求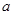 的取值范围;
的取值范围;
(3)设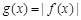 ,当
,当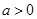 时,求函数
时,求函数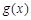 的单调减区间.
的单调减区间.
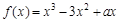
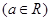 .
.(1)当
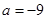 时,求函数
时,求函数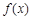 的极大值;
的极大值;(2)若函数
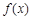 的图象与函数
的图象与函数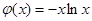 的图象有三个不同的交点,求
的图象有三个不同的交点,求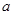 的取值范围;
的取值范围;(3)设
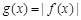 ,当
,当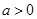 时,求函数
时,求函数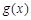 的单调减区间.
的单调减区间.(1)5;(2) ;(3)①当
;(3)①当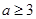 时,函数
时,函数 的单调减区间为
的单调减区间为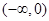 ;
;
②当 时,函数
时,函数 的单调减区间为
的单调减区间为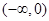 ,
,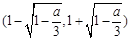 ;
;
③当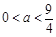 时,函数
时,函数 的单调减区间为
的单调减区间为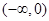 ,
, ,
, 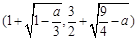 .
.
 ;(3)①当
;(3)①当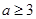 时,函数
时,函数 的单调减区间为
的单调减区间为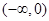 ;
; ②当
 时,函数
时,函数 的单调减区间为
的单调减区间为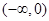 ,
,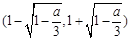 ;
; ③当
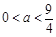 时,函数
时,函数 的单调减区间为
的单调减区间为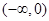 ,
, ,
, 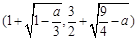 .
.试题分析:(1)当
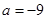 时,函数
时,函数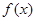 是一个具体的三次函数,只须求出
是一个具体的三次函数,只须求出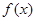 的导函数,并令它为零求得其根;然后列出
的导函数,并令它为零求得其根;然后列出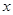 的取值范围与
的取值范围与 的符号及
的符号及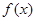 单调性的变化情况表,由此表可求得函数
单调性的变化情况表,由此表可求得函数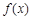 的极大值;(2)函数
的极大值;(2)函数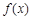 的图象与函数
的图象与函数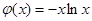 的图象有三个不同的交点,等价于方程
的图象有三个不同的交点,等价于方程 即
即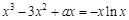 有三个不同的实数根,也等价于方程
有三个不同的实数根,也等价于方程 有三个不同的实数根,从而可转化为直线
有三个不同的实数根,从而可转化为直线 与函数
与函数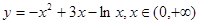 有三个不同的交点,画草图可知必须且只需:
有三个不同的交点,画草图可知必须且只需: ,所以利用导数求出函数
,所以利用导数求出函数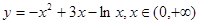 的极小值和极大值即可;(3)注意到函数
的极小值和极大值即可;(3)注意到函数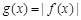 的图象与函数
的图象与函数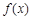 的图象之间的关系:将函数
的图象之间的关系:将函数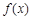 在x轴上方的图象不变,而将x轴下方的图象沿x轴翻折到x轴上方即得函数
在x轴上方的图象不变,而将x轴下方的图象沿x轴翻折到x轴上方即得函数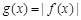 的图象,由此可知要求函数
的图象,由此可知要求函数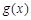 的单调减区间,只须先求出函数
的单调减区间,只须先求出函数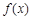 的单调区间,并求出
的单调区间,并求出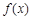 的所有零点,结合图象就可写出函数
的所有零点,结合图象就可写出函数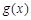 的单调减区间;注意分类讨论.
的单调减区间;注意分类讨论.试题解析:(1)当
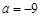 时,由
时,由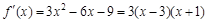 =0,得
=0,得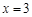 或
或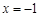 , 2分
, 2分列表如下:
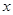 |  | -1 |  | 3 |  |
 | + | 0 | - | 0 | + |
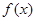 | 递增 | 极大 | 递减 | 极小 | 递增 |
所以当
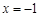 时,函数
时,函数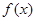 取得极大值为5. 4分
取得极大值为5. 4分(2)由
 ,得
,得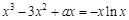 ,即
,即 , 6分
, 6分令
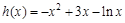 ,则
,则 ,
,列表,得
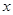 | 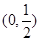 |  | 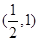 | 1 |  |
 | - | 0 | + | 0 | - |
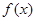 | 递减 | 极小值 | 递增 | 极大值2 | 递减 |
由题意知,方程
 有三个不同的根,故
有三个不同的根,故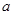 的取值范围是
的取值范围是 . 10分
. 10分(3)因为
 ,
,所以当
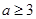 时,
时,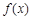 在R上单调递增;
在R上单调递增;当
 时,
时,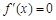 的两根为
的两根为 ,且
,且 ,
,所以此时
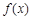 在
在 上递增,在
上递增,在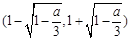 上递减,在
上递减,在 上递增;12分
上递增;12分令
 ,得
,得 ,或
,或 (*),
(*),当
 时,方程(*)无实根或有相等实根;当
时,方程(*)无实根或有相等实根;当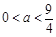 时,方程(*)有两根
时,方程(*)有两根 , 13分
, 13分从而
①当
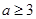 时,函数
时,函数 的单调减区间为
的单调减区间为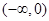 ; 14分
; 14分②当
 时,函数
时,函数 的单调减区间为
的单调减区间为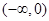 ,
,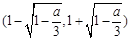 ; 15分
; 15分③当
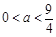 时,函数
时,函数 的单调减区间为
的单调减区间为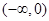 ,
, ,
, 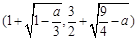 . 16分
. 16分
练习册系列答案
相关题目
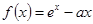 (
(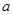 为常数)的图像与
为常数)的图像与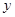 轴交于点
轴交于点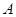 ,曲线
,曲线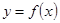 在点
在点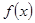 的极值;(2)证明:当
的极值;(2)证明:当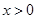 时,
时,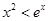 ;
;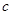 ,总存在
,总存在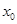 ,使得当
,使得当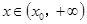 ,恒有
,恒有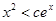 .
.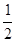
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).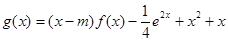 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.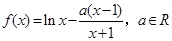 .
.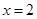 是函数
是函数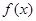 的极值点,求曲线
的极值点,求曲线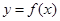 在点
在点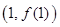 处的切线方程;
处的切线方程;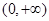 上为单调增函数,求
上为单调增函数,求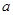 的取值范围.
的取值范围.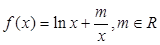 .
.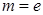 (
(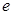 为自然对数的底数)时,求
为自然对数的底数)时,求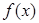 的最小值;
的最小值;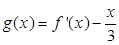 零点的个数;
零点的个数;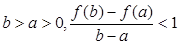 恒成立,求
恒成立,求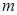 的取值范围.
的取值范围.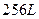 的有盖方底的水箱,它的底边长为多少时,用料最省?
的有盖方底的水箱,它的底边长为多少时,用料最省?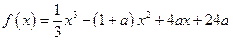 ,其中常数
,其中常数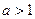
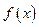 的单调性;
的单调性;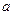 的取值范围.
的取值范围.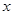 的不等式
的不等式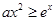 的解集中的正整数解有且只有3个,则实数
的解集中的正整数解有且只有3个,则实数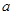 的取值范围是 .
的取值范围是 .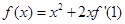 ,则
,则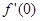 = .
= .