题目内容
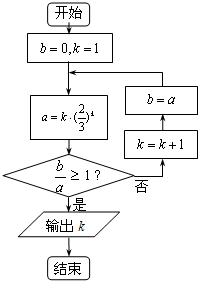（2013•丰台区一模）执行如图的程序框图，输出k的值是（ ）分析：由已知可得k←1，b←0，则a=1×(
)0=1，可得
=
=0＜1，不满足判断框的条件，应继续循环；b←1=a，再计算判断是否满足
≥1，直到满足此条件即可停止循环，输出k的值．
| 2 |
| 3 |
| b |
| a |
| 0 |
| 1 |
| b |
| a |
解答：解：①k←1，b←0，则a=1×(
)0=1，∴
=
=0＜1，不满足判断框的条件，应继续循环；
②k←2，b←1，则a=2×(
)1=
，∴
=
=
＜1，不满足判断框的条件，应继续循环；
③k←3，b←
，则a=3×(
)
=
，则
=
＞1，满足判断框的条件，应停止循环．
故输出的k是3．
故选A．
| 2 |
| 3 |
| b |
| a |
| 0 |
| 1 |
②k←2，b←1，则a=2×(
| 2 |
| 3 |
| 4 |
| 3 |
| b |
| a |
| 1 | ||
|
| 3 |
| 4 |
③k←3，b←
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| ||
| b |
| a |
| |||||
|
故输出的k是3．
故选A．
点评：正确理解循环结构的功能和判断框的条件是解题的关键．
练习册系列答案
相关题目
（2013•丰台区一模）执行右边的程序框图所得的结果是（ ）