题目内容
若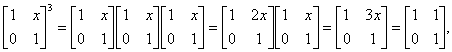
试比较x0.7与x0.8的大小.
思路解析：这里的关键是求出x的值,首先根据矩阵运算的定义建立等式,求出x再代入利用指数函数的性质即可.
解：∵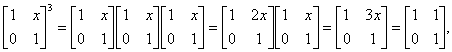
∴3x=1.∴x=
.考察y=(
)x的图象和性质得x0.7＜x0.8 .
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
试比较x0.7与x0.8的大小.100分闯关期末冲刺系列答案名校联盟快乐课堂系列答案题目内容
若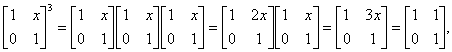试比较x0.7与x0.8的大小.
思路解析：这里的关键是求出x的值,首先根据矩阵运算的定义建立等式,求出x再代入利用指数函数的性质即可.
解：∵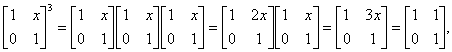
∴3x=1.∴x=.考察y=()x的图象和性质得x0.7＜x0.8 .
100分闯关期末冲刺系列答案名校联盟快乐课堂系列答案
,a≠1).记区间Dn=［1,an］(an＞1).当x∈Dn时,曲线C上存在点Pn(xn,f(xn)),使得点Pn处的切线与直线AAn平行.
Dn+1对一切n∈N*恒成立时,求实数a的取值范围;
时,试比较Sn与n+7的大小,并说明你的结论.