题目内容
抛物线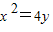 的焦点坐标是( )
的焦点坐标是( )A.(2,0)
B.(0,2)
C.(l,0)
D.(0,1)
【答案】分析:先根据标准方程求出p值,判断抛物线x2=4y的开口方向及焦点所在的坐标轴,从而写出焦点坐标.
解答:解:∵抛物线x2 =4y 中,p=2,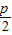 =1,
=1,
焦点在y轴上,开口向上,
∴焦点坐标为 (0,1 ),
故选D.
点评:本题考查抛物线的标准方程和简单性质的应用,抛物线 x2=2p y 的焦点坐标为(0,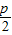 ),属基础题.
),属基础题.
解答:解:∵抛物线x2 =4y 中,p=2,
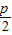 =1,
=1,焦点在y轴上,开口向上,
∴焦点坐标为 (0,1 ),
故选D.
点评:本题考查抛物线的标准方程和简单性质的应用,抛物线 x2=2p y 的焦点坐标为(0,
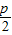 ),属基础题.
),属基础题. 
练习册系列答案
相关题目
抛物线y2=
x关于直线x-y=0对称的抛物线的焦点坐标是( )
| 1 |
| 4 |
| A、(1,0) | ||
B、(0,
| ||
| C、(0,1) | ||
D、(
|
抛物线y2=
x关于直线x-y=0对称的抛物线的焦点坐标是( )
| 1 |
| 4 |
| A、(1,0) | ||
B、(
| ||
| C、(0,1) | ||
D、(0,
|